Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




Đáp án C
Tam giác ABC có góc A là góc tù nên 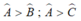
Mà cạnh đối diện với góc A là cạnh BC .
Áp dụng định lí: trong 1 tam giác cạnh đối diện với góc lớn hơn thì lớn hơn ta được:
BC > AC và BC > AB
Vậy tam giác ABC có độ dài cạnh BC là lớn nhất nên dây BC gần tâm nhất.
Chưa thể kết luận dây nào xa tâm nhất.

a) Ta có: ΔABC cân tại A
mà AH là đường cao ứng với cạnh BC
nên AH là đường trung tuyến ứng với cạnh BC
Ta có: AB=AC
nên A nằm trên đường trung trực của BC\(\left(1\right)\)
Ta có: OB=OC
nên O nằm trên đường trung trực của BC\(\left(2\right)\)
Ta có: HB=HC
nên H nằm trên đường trung trực của BC(3)
Từ (1), \(\left(2\right),\left(3\right)\) suy ra A,O,H thẳng hàng
\(\Leftrightarrow A,O,H,D\) thẳng hàng
hay AD là đường kính của \(\left(O\right)\)

Bài 1:
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2\)=\(AB^2+AC^2\)
⇔\(BC^2\)= 52 + 122 =169
hay BC = 13cm
Ta có: ΔABC vuông tại A
nên bán kính đường tròn ngoại tiếp ΔABC là một nửa của cạnh huyền BC
hay R = \(\dfrac{BC}{2}\)= \(\dfrac{13}{2}\) =6.5(cm)
Ta có:
\(\widehat{A}=108^o\)
\(\widehat{B}=18^o\)
\(\Rightarrow\widehat{C}=180^o-108^o-18^o=54^o\)
Ta có:
\(\widehat{AOB}=2\widehat{ACB}=108^o\)
\(\widehat{AOC}=2\widehat{ABC}=36^o\)
\(\Rightarrow\widehat{OAC}=\dfrac{180^o-36^o}{2}=72^o\)
\(\widehat{OAB}=\dfrac{180^o-72^o}{2}=36^o\)
Kẻ \(OH\text{⊥}AC\Rightarrow AH=OA\)
\(\cos\widehat{OAC}=10cos72^o\)
\(\Rightarrow\text{ }AC=2AH=20cos72^o\)
\(\text{Tương tự:}AB=20\cos36^o\)
\(\Rightarrow AB-AC=10cm\)