Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

-Cách 2: -Kẻ MH vuông góc với AB; MK vuông góc với AC( H thuộc AB và K thuộc AC).
-Ta có: tam giác AHM= tam giác AKM( cạnh huyền-góc nhọn).
=> HM=MK. => tam giác BHM= tam giác CKM( cạnh huyền-cạnh góc vuông).
=> góc HBM= góc KCM. => tam giác ABC cân tại A.(đpcm)

Xét tam giác ABM VÀ ACM:
Góc MAB= MAC ( do AM là tia phân giác)
AM: cạnh chung'
BM=BC ( do M là trung điểm BC)
=> tam giác ABM= ACM ( c.g.c)
vậy: AB=AC ( hai cạnh tương ứng)
suy ra: Tam giác ABC là tam giác cân

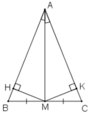
Kẻ MH ⊥ AB, MK ⊥ AC
Xét hai tam giác vuông AHM và AKM, ta có:
∠(AHM) =∠(AKM) = 90o
Cạnh huyền AM chung
∠(HAM) = ∠KAM) (gt)
⇒ ΔAHM = ΔAKM (cạnh huyền, góc nhọn)
Suy ra: MH = MK (hai cạnh tương ứng)
Xét hai tam giác vuông MHB và MKC, ta có:
∠(MHB) = ∠(MKC) = 90o
MB = MC ( vì M là trung điểm BC).
MH = MK (chứng minh trên)
⇒ ΔMHB = ΔMKC (cạnh huyền, cạnh góc vuông)
Suy ra: ∠B = ∠C (hai góc tương ứng)
Vậy tam giác ABC cân tại A.

Vì M là trung điểm của BC
=> BM = MC
Xét \(\Delta ABM\)và \(\Delta ACM\) có:
\(\widehat{BAM}=\widehat{CAM}\) ( AM là tia phân giác \(\widehat{A}\) )
AM (chung)
BM = CM (cmt)
Do đó: \(\Delta ABM=\Delta ACM\left(c-g-c\right)\)
=> AB = AC (hai cạnh tương ứng)
=> \(\Delta ABC\) cân tại A

xét tam giác ABM và tam giác ACM CO
MB=MC
AM CHUNG
GOC M CHUNG
=> TAM GIC ABM = TAM GIÁC AMC
=>AB=AC
=> TAM GIÁC ABC CÂN TẠI A

thì vừa là đường trung tuyến vừa là đường trung trực thì tam giác đó cân chứ sao trời!

a)

Xét 2 tam giác vuông AMC và AMB có:
AM chung
BM=CM (gt)
=>\(\Delta AMC = \Delta AMB\) (hai cạnh góc vuông)
=> AC=AB (2 cạnh tương ứng)
=> Tam giác ABC cân tại A
b)

Kẻ MH vuông góc với AB (H thuộc AB)
MG vuông góc với AC (G thuộc AC)
Xét 2 tam giác vuông AHM và AGM có:
AM chung
\(\widehat {HAM} = \widehat {GAM}\) (do AM là tia phân giác của góc BAC)
=>\(\Delta AHM = \Delta AGM\) (cạnh huyền – góc nhọn)
=> HM=GM (2 cạnh tương ứng)
Xét 2 tam giác vuông BHM và CGM có:
BM=CM (giả thiết)
MH=MG(chứng minh trên)
=>\(\Delta BHM = \Delta CGM\)(cạnh huyền – cạnh góc vuông)
=>\(\widehat {HBM} = \widehat {GCM}\)(2 góc tương ứng)
=>Tam giác ABC cân tại A.

a: Xét ΔABD và ΔACE có
AB=AC
góc ABD=góc ACE
BD=CE
=>ΔABD=ΔACE
b: ΔABD=ΔACE
=>AD=AE
=>ΔADE cân tại A
c: ΔABC cân tại A
mà AM là trung tuyến
nên AM vuông góc BC
ΔADE cân tại A
mà AM vuông góc DE
nên AM là phân giác của góc DAE
d: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
góc BAH=góc CAK
=>ΔAHB=ΔAKC
=>AH=AK
=>ΔAHK cân tại A
B C A H D 1 2 1 2
Trời ạ, lại bắt vẽ hình. Thầy mk vẽ một cái hình tam giác kiểu này cũng phải mất chừng 30 phút mới vẽ đúng đc. Nhưng thôi, mk vẽ kiểu này chắc bạn cũng hiểu rồi hen, có ký hiệu đàng hoàng mà. À mà bài này do dữ liệu cho trước ko liên quan j tới nhau nên phải vẽ thêm HD nữa.
Bài làm
Trên tia đối của tia AH, vẽ HD = AH.
Xét tam giác ABH và tam giác HCD, ta thấy:
suy ra: tam giác ABH = tam giác DCH (c.g.c.)
suy ra:
Mà \(\widehat{A_1}=\widehat{A_2}\)(gt)
=> \(\widehat{A_2}=\widehat{D}\)
=> tam giác ACD cân tại C
=> CD = AC (2)
Từ (1) và (2) suy ra:
AB = AC
=> tam giác ABC cân tại A