Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

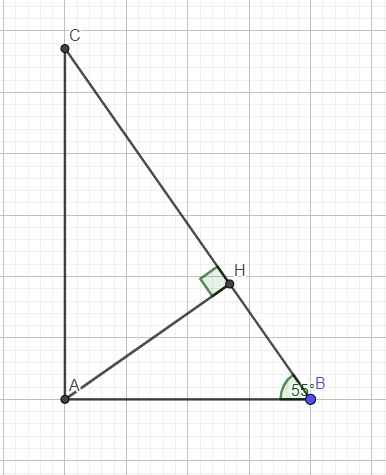
Trong tam giác vuông ABC:
\(cosB=\dfrac{AB}{BC}\Rightarrow AB=BC.cosB\)
Trong tam giác vuông ABH:
\(sinB=\dfrac{AH}{AB}\Rightarrow AH=AB.sinB=BC.sinB.cosB=6.sin55^0.cos55^0\approx2,8\left(cm\right)\)
\(cosB=\dfrac{BH}{AB}\Rightarrow BH=AB.cosB=BC.\left(cosB\right)^2=6.\left(cos55^0\right)^2\approx1,2\left(cm\right)\)
\(CH=BC-BH=6-1,2=4,8\left(cm\right)\)

Áp dụng định lý Pi-ta-go cho \(\Delta ABH\)vuông tại H ta có :
\(BH^2=AB^2-AH^2\)
\(\Leftrightarrow BH^2=13^2-5^2\)
\(\Leftrightarrow BH^2=144\)
\(\Leftrightarrow BH=12\)
Áp dụng hệ thức lượng trong tam giác ta có :
\(AB^2=BC.BH\)
\(\Leftrightarrow13^2=BC.12\)
\(\Leftrightarrow BC=\frac{169}{12}\)
Áp dụng định lí Py-ta-go cho \(\Delta ABC\)vuông tại A ta có :
\(AC^2=BC^2-AB^2\)
\(\Leftrightarrow AC^2=\left(\frac{169}{12}\right)^2-13^2\)
\(\Leftrightarrow AC^2=\frac{4225}{144}\)
\(\Leftrightarrow AC=\frac{65}{12}\)
Ta có : \(BH+CH=BC\)
\(\Leftrightarrow CH=BC-BH=\frac{169}{12}-12=\frac{25}{12}\)
Vậy \(BC=\frac{169}{12};BH=12;AC=\frac{65}{12};CH=\frac{25}{12}\)

Ta có: \(\dfrac{AB}{AC}=\sqrt{3}\)
\(\Leftrightarrow HB=3\cdot HC\)
Ta có: \(AH^2=HB\cdot HC\)
\(\Leftrightarrow3\cdot HC=12\)
hay HC=4(cm)
\(\Leftrightarrow HB=\dfrac{4}{3}\left(cm\right)\)
\(\Leftrightarrow BC=\dfrac{16}{3}\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB=\dfrac{8}{3}\left(cm\right)\\AC=\dfrac{8\sqrt{3}}{3}\left(cm\right)\end{matrix}\right.\)

BC = BH + HC = 175 km
Áp dụng Hệ thức lượng trong tam giác vuông ABC có: AB2 = BH.BC = 63.175 => AB = 105 km
AC2 = CH. BC = 112. 175 => AC = 140 km
AD là p/g của góc A => BD / DC = AB/ AC = 105/140 = 3/4 => BD = 3/4 . DC
Mà BD + DC = BC = 175 => 3/4 . DC + DC = 175 => 7/4 . DC = 175 => DC = 175 : 7/4 = 100
Vì CD < CH => D nằm giữa C và H => DH = CH - CD = 112 - 100 = 12 km
A=1.2.3+2.3.4+3.4.5+...+98.99.1004A=1.2.3.4+2.3.4.4+3.4.5.4+...+98.99.100.44A=1.2.3.(4-0)+2.3.4.(5-1)+...+98.99.100.(101-97)4A=1.2.3.4+2.3.4.5-1.2.3.4+...+98.99.100.101-97.98.99.1004A=1.2.3.4-1.2.3.4+2.3.4.5-...-97.98.99.100+98.99.100.1014A=98.99.100.1014A=97990200A=979902004A=24497550

Xét \(\Delta ABH\)và \(\Delta CAH\)có
\(\widehat{AHB}=\widehat{CHA}=90^0\)
\(\widehat{BAH}=\widehat{ACH}\) (cùng phụ với góc HAC)
suy ra: \(\Delta ABH~\Delta CAH\) (g.g)
suy ra: \(\frac{AB}{AC}=\frac{AH}{CH}=\frac{BH}{AH}\)
hay \(\frac{5}{6}=\frac{30}{CH}=\frac{BH}{30}\)
suy ra: \(CH=\frac{6.30}{5}=36\)
\(BH=\frac{5.30}{6}=25\)

BH =x<0
HC = 25-x
AH2=BH .HC
AH2 = x(25-x)
144=25x-x2
X2=25x+144
x2-25x+144
x2-9x-16x+144=0
(x-16)(x-9)=0
suy ra x=16;x=9
nếu BH =16 suy ra HC =25-16=9
AB2=BC.BH
AB2=25.16
AB2=căn 400=20
nếu BH =9 suy ra 25-9=16
AB2=25.9
AB=căn 225=15

\(\left[{}\begin{matrix}\\\\\\\end{matrix}\right.\prod\limits^{ }_{ }\int_{ }^{ }dx\sinh_{ }^{ }⋮\begin{matrix}&&&\\&&&\\&&&\\&&&\\&&&\\&&&\end{matrix}\right.\Cap\begin{matrix}&&\\&&\\&&\\&&\\&&\\&&\end{matrix}\right.\)