Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CÂU HỎI GÌ MÀ KÌ VẬN TỐC LÚC ĐI VÀ VỀ SAO KHÔNG HỀ THAY ĐỖI.
luc di vs luc ve van toc trung binh bang nhau thi sao ma to tinh cho cau dc
Àk mình zỏi văn chứ ko zỏi toán nha bn. Ko bík thì lên mạng hỏi thui. :)
Gọi vận tốc của người đó khi đi là x km/h(x > 6)
Vận tốc khi về là x – 6 (km/h)
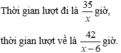
Vì thời gian lượt về bằng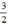 
thời gian lượt đi nên ta có phương trình:
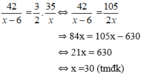
Vậy vận tốc lượt đi của người đó là 30km/h, vân tốc lượt về là 24km/h
Gọi độ dài quãng đường từ nhà đến trường là x(km)(Điều kiện: x>0)
Thời gian học sinh đi từ nhà đến trường:
\(\dfrac{x}{15}\left(h\right)\)
Thời gian học sinh đi từ trường về nhà:
\(\dfrac{x}{12}\left(h\right)\)
Theo đề, ta có phương trình: \(\dfrac{x}{12}-\dfrac{x}{15}=\dfrac{1}{6}\)
\(\Leftrightarrow\dfrac{5x}{60}-\dfrac{4x}{60}=\dfrac{10}{60}\)
\(\Leftrightarrow5x-4x=10\)
hay x=10(thỏa ĐK)
Vậy: Độ dài quãng đường từ nhà đến trường là 10km
Gọi qđ từ nhà đến trg là: x ( x>0) (km)
T/g lúc đi từ nhà đến trg là : x/15 (h)
T/g lúc đi từ trg về nhà là: x/12 (h)
Ta có pt:
x/15 + 1/6 = x/12
=>( 6x+15) / 90 = x/12
=> 72x + 180 = 90x
=> 180 = 8x
=> x = 22,5
Đổi 10 phút=1/6 giờ
Gọi quãng đường cần tìm là x (>0,km)
Thời gian đi từ nhà đến trường là : x/15(h)
Thời gian đi từ trường về nhà là: x/12 (h)
Theo bài ra ta có: x/12=x/15+1/6 <=> x=10 (km) (thỏa mãn)
Vậy:...
a) Phân thức biểu thị thời gian xe chạy trong thành phố: \({t_1} = \frac{{20}}{x}\) (giờ)
Phân thức biểu thị thời gian xe chạy trên đường cao tốc: \({t_2} = \frac{{50}}{{x + 55}}\) (giờ)
b)Phân thức biểu thị tổng thời gian chú Đức đi từ Hà Nội về quê:
\(\begin{array}{l}{t_1} + {t_2} + \frac{1}{4}\\ = \frac{{20}}{x} + \frac{{50}}{{x + 55}} + \frac{1}{4}\\ = \frac{{80\left( {x + 55} \right) + 200{\rm{x}} + x\left( {x + 55} \right)}}{{4{\rm{x}}\left( {x + 55} \right)}} = \frac{{{x^2} + 335{\rm{x}} + 4400}}{{4{\rm{x}}\left( {x + 55} \right)}}\end{array}\)
\(45ph=\dfrac{3}{4}\left(h\right)\)
Gọi thời gian đi là x>0 (giờ) \(\Rightarrow\) thời gian về là \(x+\dfrac{3}{4}\) (giờ)
Quãng đường lúc đi: \(15x\) (km)
Quãng đường lúc về: \(12\left(x+\dfrac{3}{4}\right)\) (km)
Do quãng đường AB là ko đổi nên ta có pt:
\(15x=12\left(x+\dfrac{3}{4}\right)\Leftrightarrow3x=9\Rightarrow x=3\) (giờ)
Độ dài quãng đường AB: \(S=15.3=45\left(km\right)\)
a) Thời gian Tâm đi là: \(\dfrac{{15}}{x}\) (giờ)
Tốc độ Tâm đi lúc về là: \(x + 4\) (km/h)
Thời gian Tâm về là: \(\dfrac{{15}}{{x + 4}}\) (giờ)
Tổng thời gian lượt đi và về là:
\(T = \dfrac{{15}}{x} + \dfrac{{15}}{{x + 4}} = \dfrac{{15\left( {x + 4} \right)}}{{x\left( {x + 4} \right)}} + \dfrac{{15x}}{{x\left( {x + 4} \right)}} = \dfrac{{15x + 60 + 15x}}{{x\left( {x + 4} \right)}} = \dfrac{{30x + 60}}{{{x^2} + 4x}}\)
b) Hiệu thời gian đi và về là:
\(t = \dfrac{{15}}{x} - \dfrac{{15}}{{x + 4}} = \dfrac{{15\left( {x + 4} \right)}}{{x\left( {x + 4} \right)}} - \dfrac{{15x}}{{x\left( {x + 4} \right)}} = \dfrac{{15x + 60 - 15x}}{{x\left( {x + 4} \right)}} = \dfrac{{60}}{{{x^2} + 4x}}\)
c) Thay \(x = 10\) vào \(T\) và \(t\) ta có:
\(T = \dfrac{{30.10 + 60}}{{{{10}^2} + 4.10}} = \dfrac{{360}}{{140}} = \dfrac{{19}}{7}\)
\(t = \dfrac{{60}}{{{{10}^2} + 4.10}} = \dfrac{{60}}{{140}} = \dfrac{3}{7}\)