Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì một phần cơ năng của quả bóng đã chuyển hoá thành nội năng của bóng, sân và không khí:
∆ U = E 1 - E 2 = mg( h 1 - h 2 ) = 2,94 J

Chọn chiều dương hướng xuống mặt đất
Vận tốc khi chạm đất : \(v=\sqrt{2gh}=4\left(m\backslash s\right)\)
Vận tốc sau khi va chạm \(0,01s\) : \(v_1=v+gt=3,9\left(m\backslash s\right)\)
Độ biến thiên động lượng trong thời gian va chạm :
\(\Delta p=p'-p=m\left(-v'\right)-mv=-0,0395\left(kg.m\backslash s\right)=F.\Delta t\)
\(\Leftrightarrow F=-3,95\left(N\right)\)

Đáp án C
Ap dụng công thức
Thời gian để vật đạt độ cao cực đại : t 1 = v 0 g
Thời gian để vật quay về điểm ném : t 1 = v 0 g
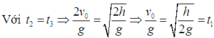

Áp dụng định luật bảo toàn cơ năng đối với hai trường hợp chuyển động của quả bóng:
- Khi quả bóng rơi tự do từ độ cao h 1 xuống chạm đất: mg h 1 = m v 1 2 /2
Trong đó m là khối lượng của quả bóng, v 1 là vận tốc của vật ngay trước khi chạm đất:


a) Độ dốc của đường thẳng có giá trị bằng gia tốc
AB và DE đều là đường thẳng nên gia tốc không đổi, vì vậy độ dốc của đoạn thẳng AB giống độ dốc của đoạn thẳng DE
b) Diện tích tam giác ABC biểu diễn quãng đường dịch chuyển của quả bóng từ A đến B
c) Diện tích tam giác ABC biểu diễn quãng đường dịch chuyển của vật từ A đến B
Diện tích tam giác CDE biểu diễn quãng đường dịch chuyển của vật từ D đến E
Trong quá trình chuyển động của quả bóng thì cơ năng được bảo toàn, nhưng khi quả bóng đi từ A đến B thì năng lượng của quả bóng bị mất đi do một phần bị tỏa nhiệt, vì vậy năng lượng của quả bóng giảm đi nên khi quả bóng đi từ D đến E thì quãng đường DE ngắn hơn quãng đường AB. Vì vậy diện tích tam giác ABC lớn hơn diện tích tam giác CDE.

Đầu tiên, ta xác định các biến:
h: độ cao ban đầu của quả bóng (m)α: góc nghiêng của mặt phẳng nghiêng so với mặt phẳng ngang (đơn vị góc)v: vận tốc của quả bóng sau khi va chạm tại mỗi lần nảy lên (m/s)l1: khoảng cách giữa các điểm rơi liên tiếp từ lần thứ nhất đến lần thứ hai (m)l2: khoảng cách giữa các điểm rơi liên tiếp từ lần thứ hai đến lần thứ ba (m)l3: khoảng cách giữa các điểm rơi liên tiếp từ lần thứ ba đến lần thứ tư (m)Giả sử quả bóng rơi tự do từ độ cao h xuống mặt phẳng nghiêng. Khi va chạm tuyệt đối đàn hồi với mặt phẳng nghiêng, năng lượng và động lượng của quả bóng được bảo toàn.
Ta có công thức tính năng lượng và động lượng của quả bóng sau khi va chạm:
Năng lượng sau va chạm = Năng lượng trước va chạm (1/2)mv^2 = mgh
Động lượng sau va chạm = Động lượng trước va chạm mv = m√(2gh)
Trong đó: m: khối lượng của quả bóng (kg) g: gia tốc trọng trường (m/s^2)
Ở lần thứ nhất, quả bóng rơi từ độ cao h xuống mặt phẳng nghiêng, nên ta có: l1 = h*sin(α)
Ở lần thứ hai, quả bóng nảy lên từ mặt phẳng nghiêng, nên ta có: l2 = 2h*sin(α)*cos(α)
Ở lần thứ ba, quả bóng rơi từ độ cao h xuống mặt phẳng nghiêng, nên ta có: l3 = 2h*sin^2(α)*cos(α)
Vậy, hệ thức liên hệ giữa l1, l2 và l3 là: l1 = hsin(α) l2 = 2hsin(α)cos(α) l3 = 2hsin^2(α)*cos(α)

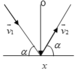
Chon chiều dương như hình vẽ theo bài ra
v 1 = v 2 = v = 10 ( m / s )
Độ biến thiên động lượng
Δ p → = p → 2 − p → 1 = m v → 2 − m v → 1
Chiếu lên chiều dương
⇒ Δ p = − m v 2 sin α − m v 1 sin α = − 2 m v sin α
Lực trung bình do sàn tác dụng lên bóng
Δ p = F . Δ t ⇒ F = Δ p Δ t
a. với α = 30 0
Ta có Δ p = − 2 m v sin α = − 2.0 , 5.10. sin 30 0 = − 5 ( k g m / s )
Lực trung bình do sàn tác dụng lên bóng
F = Δ p Δ t = − 5 0 , 1 = − 50 ( N )
b. Với α = 90 0
Ta có Δ p = − 2 m v sin α = − 2.0 , 5.10. sin 90 0 = − 10 ( k g m / s )
Lực trung bình do sàn tác dụng lên bóng
F = Δ p Δ t = − 10 0 , 1 = − 100 ( N )

a: Tốc độ của quả bóng ngay trước khi chạm đất là:
\(v=\sqrt{2\cdot g\cdot h}=\sqrt{2\cdot9.81\cdot1.2}\simeq4,5\)(m/s)
b: Tốc độ của quả bóng ngay khi bắt đầu bật lên là:
\(v=g\cdot t=9.81\cdot0.16\simeq1,57\)(m/s)
c:
Gia tốc có phương thẳng đứng.
Độ lớn là:\(a=\dfrac{\left|1.57-4.85\right|}{0.16}\simeq20,5\)(m/s)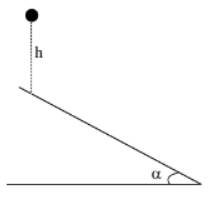

Khi thả quả bóng xuống mặt sàn, khi nảy lên, bóng không thể lên tới độ cao ban đầu vì trong quá trình chuyển hóa, cơ năng của quả bóng đã chuyển thành nhiệt năng. Cơ năng không được bảo toàn, vì vậy quả bóng không nảy lên được độ cao ban đầu.