Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét ΔABC vuông tại B có \(tanC=\dfrac{AB}{BC}\)
=>\(AB=BC\cdot tanC=12\cdot tan35\simeq8,4\left(m\right)\)

Gọi chân cột đèn là điểm A, đỉnh cột đèn là điểm B và bóng của đỉnh cột trên mặt đất là C
Ta có tam giác ABC vuông tại A với \(AC=7,5\left(m\right)\) và \(\widehat{BCA}=42^0\)
Trong tam giác vuông ABC:
\(AB=AC.tan\widehat{BAC}=7,5.tan42^0\approx6,8\left(m\right)\)

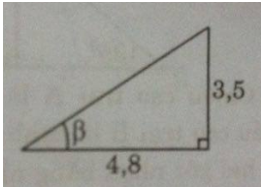
Chiều cao cột cờ là cạnh đối diên với góc giữa tia sang mặt trời và bóng cột cờ, chiều dài bóng là cạnh kề góc nhọn.
\(\tan B=\dfrac{35}{48}\)nên \(\widehat{B}=36^06'\)
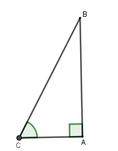
Ta có: tan C = A B A C = 7 4 ⇒ C ^ ≃ 60 0 15 '
Đáp án cần chọn là: D

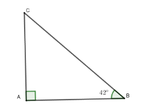
Ta có chiều cao cột đèn là AC; AB = 7,5m và A C B ^ = 42 0
Xét tam giác ACB vuông tại A có:
AC = AB. tan B = 7,5. tan 42 0 ≈ 6,753m
Vậy cột đèn cao 6,753m
Đáp án cần chọn là: A
