Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Vì ABCD là hình bình hành nên AB // CD.
Tứ giác AMCN có AM // CN (vì AB // CD); AM = CN (giả thiết).
Suy ra, tứ giác AMCN là hình bình hành.
Do đó AN = CM (đpcm).
b) Vì tứ giác AMCN là hình bình hành suy ra \(\widehat {AMC} = \widehat {ANC}\) (đpcm).

a/kẻ AC, vì BC//AD nên \(S_{ADN}=S_{ADC}\left(1\right)\)( chung đáy AD)
Vì AB//CD nên \(S_{ADC}=S_{DMC}\left(2\right)\)( chung đáy DC)
Từ (1) vfa (2) suy ra ĐPCM
b/Kẻ DH vuông góc AN tại H, DK vuông góc CM tại K
\(S_{ADN}=S_{DMC}\&AN=CM\Rightarrow DH=DK\)
Xét tgiac DHI và DKI đều vuông có: DH=DK, chung DI
Suy ra \(\Delta DHI=\Delta DKI\Rightarrow\widehat{AID}=\widehat{DIC}\)

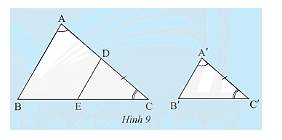
a) Vì \(ED//AB \Rightarrow \Delta DEC\backsim\Delta ABC\) (định lí)
b) Vì \(ED//AB \Rightarrow \widehat {CDE} = \widehat {CAB}\) (hai góc đồng vị)
Mà \(\widehat {CAB} = \widehat {A'}\). Do đó, \(\widehat {CDE} = \widehat {B'A'C'}\).
Xét tam giác \(A'B'C'\) và tam giác \(DEC\) ta có:
\(\widehat {B'A'C'} = \widehat {CDE}\) (chứng minh trên)
\(A'C' = CD\) (giải thuyết)
\(\widehat {C'} = \widehat C\) (giả thuyết)
Do đó, \(\Delta A'B'C' = \Delta DEC\) (g.c.g)
c) Vì tam giác \(\Delta A'B'C'\backsim\Delta DEC\) (tính chất)
Mà \(\Delta DEC\backsim\Delta ABC\) nên \(\Delta ABC\backsim\Delta A'B'C'\).

Câu hỏi của Truong Tuan Dat - Toán lớp 8 - Học toán với OnlineMath
Em sai đề rồi nhé! Tham khảo đề bài và bài làm tại link này nhé em