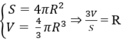K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
AH
Akai Haruma
Giáo viên
19 tháng 12 2017
Lời giải:
\(a+b=3\Rightarrow a+(b-2)=1\Rightarrow b-2=1-a\)
Ta có:
\(f(x)=\frac{9^x}{9^x+3}\Rightarrow f(a)=\frac{9^a}{9^a+3}\) (1)
\(f(b-2)=f(1-a)=\frac{9^{1-a}}{9^{1-a}+3}=\frac{9}{9^a\left(\frac{9}{9^a}+3\right)}\)
\(=\frac{9}{9+3.9^a}=\frac{3}{3+9^a}\) (2)
Từ (1),(2) suy ra \(f(a)+f(b-2)=\frac{9^a}{9^a+3}+\frac{3}{3+9^a}=\frac{9^a+3}{9^a+3}=1\)
Đáp án A
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 3 2023
\(\int\limits^5_3\dfrac{dx}{x^2-x}=\int\limits^5_3\dfrac{dx}{x\left(x-1\right)}=\int\limits^5_3\left(\dfrac{1}{x-1}-\dfrac{1}{x}\right)dx\)
\(=\left(ln\left(x-1\right)-lnx\right)|^5_3=ln4-ln5-\left(ln2-ln3\right)\)
\(=2ln2-ln5-ln2+ln3\)
\(=-ln5+ln3+ln2\)
\(\Rightarrow a=-1;b=1;c=1\)
CM
24 tháng 1 2018
Chọn C.
Dựa vào công thức diện tích mặt cầu và thể tích hình cầu, ta có:
