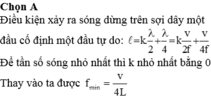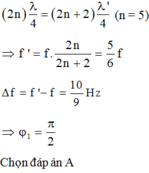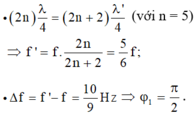Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án A
Dây đàn một đầu cố định, một đầu tự do, để có sóng dừng trên dây thì:
L = k . λ 2 + λ 4 = 2 k + 1 λ 4 = 2 k + 1 v 4 f ⇒ f = 2 k + 1 v 4 L
⇒ f min = v 4 L k h i k = 1

Đáp án D
Điều kiện để có sóng dừng trên dây một đầu cố định, một đầu tự do là:
![]()
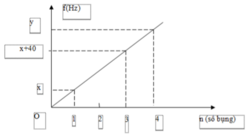
Số bụng sóng là: n = k+1.
Khi n = 1 thì k = 0 nên: ![]()
Khi n = 3 thì k = 2 nên:
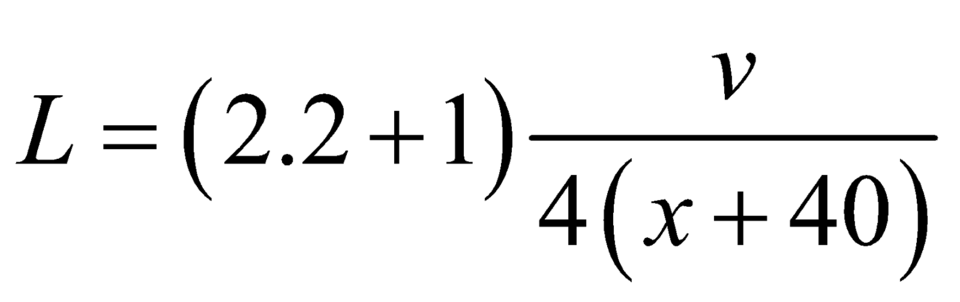
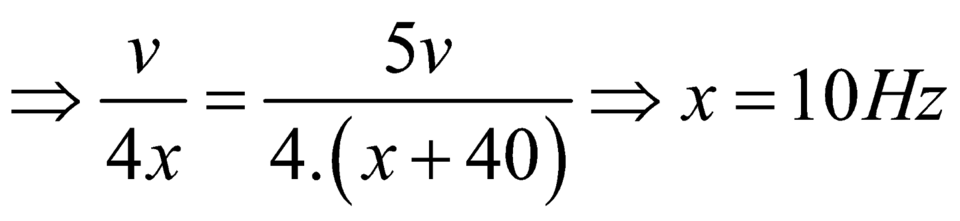
Khi n = 4 thì k = 3 nên:
![]()
![]()
Vậy trung bình cộng của x và y là:
(x+y)/2 = (10+70)/2=40Hz.

Đáp án B
+ Ban đầu: dây 2 đầu cố định ⇒ f = n . v 2 L (1)
+ Sau: dây 1 đầu cố định, 1 đầu tự do
⇒ f ' = ( 2 k + 1 ) v 4 L ⇒ f + f 12 = ( 2 k + 1 ) v 4 L f − f 12 = ( 2 k − 1 ) v 4 L
Chia (2) cho (3) tìm được k = 6.
Chia (2) cho (1) được: f + f 12 f = 2 k + 1 2 n ⇔ 13 12 = 2.6 + 1 2 n ⇔ n = 6

Đáp án A
+ Điều kiện để có sóng dừng trên dây với hai đầu cố định l = n v 2 f với n là số bó sóng trên dây.
→ n = 2 l f v = 2 . 1 , 2 . 30 24 = 3 → trên dây có 3 bụng và 4 nút.