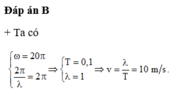Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(u=2\cos\left(20\pi\left(t-\frac{x}{25}\right)\right)=2\cos\left(20\pi t-\frac{4\pi x}{5}\right)\)
\(\Rightarrow\lambda=\frac{5}{2}\left(m\right)=250\left(cm\right)\)
\(f=\frac{\omega}{2\pi}=\frac{20\pi}{2\pi}=10\left(Hz\right)\)
\(\Rightarrow v=f.\lambda=10.250=2500\left(cm/s\right)=25\left(m/s\right)\)
Đáp án C

Ta có: \(\frac{2\pi}{\lambda}=0,02\pi\Rightarrow\lambda=100\left(cm\right)\)
\(\Rightarrow v=\lambda.f=\frac{\omega}{2\pi}\lambda=200\left(cm/s\right)\)

Ta có: \(\dfrac{2\pi.x}{\lambda}=0,02\pi.x\)
\(\Rightarrow \lambda=\dfrac{2}{0,02}=100 cm\)

Tổng quát : \(u=a\cos(2\pi f t-2\pi \frac{x}{\lambda})cm.\)\(\Rightarrow \lambda = 3m, w = \pi/3 (rad/s)\Rightarrow f = 1/6Hz.\)
\(v = \lambda.f = 3.1/6= 0.5m/s.\)

\(\omega=\frac{2\pi}{T}=2\pi\)(rad/s)
Vận tốc cực đại \(v_{max}=\omega A=2\pi.5=10\pi\)(cm/s)
Vì vận tốc là đại lượng biến thiên điều hòa theo thời gian, nên ta khảo sát nó bằng véc tơ quay.
10π v 5π M N -10π O
Tại thời điểm t, trạng thái của vận tốc ứng với véc tơ OM, sau 1/6 s = 1/6 T, véc tơ quay: 1/6.360 = 600
Khi đó, trạng thái của vận tốc ứng với véc tơ ON --> Vận tốc đạt giá trị cực đại là: \(10\pi\) (cm/s)
Đáp án B.

Đáp án: A
HD Giải: v = H e _ s o _ t r u o c _ t H e _ s o _ t r u o c _ x = 20 4 = 5 m / s

Hướng dẫn: Chọn đáp án A
Chú ý: Nếu phương trình dao động tại nguồn u = A cos ω t + β thì phương trình sóng tại M cách O một khoảng x là
u = A cos ω t + β − 2 π λ x .
1) Vận tốc dao động của phần tử vật chất tại điểm M là đạo hàm của li độ theo t:
v
=
u
t
'
=
−
ω
A
sin
ω
t
+
β
−
2
π
λ
x
2) Hệ số góc của tiếp tuyến với đường sin tại điểm M là đạo hàm li độ theo x:
tan α = u x ' = 2 π λ A sin ω t + β − 2 π λ x