Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi số đó là \(\overline{xyz}\). Theo đề bài, ta có \(2\left(yz+5\right)=x^2\) \(\Rightarrow x⋮2\)
Mà \(2\left(yz+5\right)\ge10\) nên \(x^2\ge10\Leftrightarrow x\ge4\)
\(\Rightarrow x\in\left\{4,6,8\right\}\)
Nếu \(x=4\) thì \(yz+5=8\Leftrightarrow yz=3\) \(\Rightarrow\left(y,z\right)\in\left\{\left(1;3\right),\left(3;1\right)\right\}\)
Nếu \(x=6\) thì \(yz+5=18\Leftrightarrow yz=13\), vô lí.
Nếu \(x=8\) thì \(yz+5=32\Leftrightarrow yz=27\) \(\Leftrightarrow yz\in\left\{\left(3;9\right),\left(9;3\right)\right\}\)
Vậy có 4 số thỏa mãn ycbt là 413, 431, 839, 893.

Số ngày lớn nhất trong một tháng là 31. Do đó chỉ có 1 bộ ba số nguyên tố có hai chữ số thỏa mãn đề bài là 11, 13, 17 (nếu trong 3 số có một số lớn hơn hoặc bằng 19 thì sẽ xuất hiện tổng lớn hơn 31).
Vậy ba số áo của ba nữ sinh là 11, 13, 17 và ba tổng đôi một của chúng là 24, 28 và 30.
Vì tất cả các ngày nói đến trong câu chuyện nằm trong cùng một tháng, sắp theo thứ tự: ngày sinh của Brittany; hôm nay; ngày sinh của Caitlin. Suy ra ngày hôm nay là 28 và ngày sinh của Caitlin là 30. Như vậy Caitlin mặc áo số 11 (và số áo của Asley là 13, của Brittany là 17).
Số ngày lớn nhất trong một tháng là 31, và các số nguyên tố có hai chữ số nhỏ nhất là 11, 13, 17 (các số nguyên tố tiếp theo bị loại vì tổng của nó với số nguyên tố có hai chữ số bất kỳ lớn hơn 31).
Vậy ba số áo 11, 13, 17, và ba tổng đôi một của chúng là 24, 28 và 30.
Vì tất cả các ngày nói đến trong câu chuyện nằm trong cùng một tháng, nên ngày sinh của Caitlin lớn nhất, tức là bằng 30, ngày hôm nay là 28 và ngày sinh của Bethany là 24.
Từ đó dễ dàng tìm được số áo của Asley là 13, của Bethany là 17 còn Caitlin mang áo số1 1

a) Xét hàm số \(y=ax^4+bx^2+c\)
Ta có \(y'=4ax^3+2bx=2x\left(2ax^2+b\right)\)
\(y'=0\Leftrightarrow x=0\) hoặc \(2ax^2+b=0\left(1\right)\)
Đồ thị hàm số có 3 cực trị phân biệt khi và chỉ khi \(y'=0\) có 3 nghiệm phân biệt hay phương trình (1) có 2 nghiệm phân biệt khác 0 \(\Leftrightarrow ab< 0\) (*)
Với điều kiện (*) thì đồ thị có 3 điểm cực trị là :
\(A\left(0;c\right);B\left(-\sqrt{-\frac{b}{2a},}c-\frac{b^2}{4a}\right);C\left(\sqrt{-\frac{b}{2a},}c-\frac{b^2}{4a}\right)\)
Ta có \(AB=AC=\sqrt{\frac{b^2-8ab}{16a^2}};BC=\sqrt{-\frac{2b}{a}}\) nên tam giác ABC vuông khi và chỉ khi vuông tại A.
Khi đó \(BC^2=2AB^2\Leftrightarrow b^3+8a=0\)
Do đó yêu cầu bài toán\(\Leftrightarrow\begin{cases}ab< 0\\b^3+8a=0\end{cases}\)\(\Leftrightarrow\begin{cases}-2\left(m+1\right)< 0\\-8\left(m+1\right)^3+8=0\end{cases}\)\(\Leftrightarrow m=0\)
b) Ta có yêu cầu bài toán \(\Leftrightarrow\begin{cases}ab< 0\\OA=BC\end{cases}\)\(\Leftrightarrow\begin{cases}-2\left(m+1\right)< 0\\m^2-4\left(m+1\right)=0\end{cases}\)
\(\Leftrightarrow m=2\pm2\sqrt{2}\)

Ta có : y’ = 4x3-4( m+ 1) x= 4x( x2- (m+ 1) ).
Hàm số có điểm cực trị khi và chỉ khi y’ = 0 có nghiệm phân biệt hay m+1> 0 suy ra m> - 1. (*)
Khi đó, ta có:
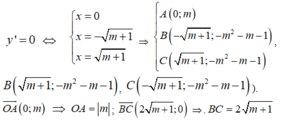
Do đó O A = B C ⇔ m = 2 m + 1 ⇔ m 2 - 4 m - 4 = 0 ( ∆ ' = 8 ) ⇔ m = 2 ± 2 2 (thỏa mãn (*)).
Vậy m = 2 ± 2 2 .
Chọn A.

Chọn A
Ta có:
![]()
Hàm số có 3 điểm cực trị khi và chỉ khi :
y ' có 3 nghiệm phân biệt
⇔ m + 1 > 0 ⇔ m > - 1 ( * )
Khi đó, ta có y ' = 0
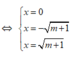
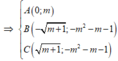
(vai trò của B, C trong bài toán là như nhau ) nên ta giả sử
![]()
Ta có: O A ( 0 ; m ) ⇒ O A = m ⇒ B C = 2 m + 1
Do đó OA = BC
![]()
![]()
⇔ m = 2 ± 2 2 ( t h ỏ a m ã n ) ( * )
Vậy m = 2 ± 2 2
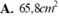
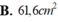
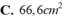
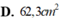

89 x 2 - 57 = bao nhiêu tự tính