Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Không gian mẫu \(\Omega\) chọn 3 thẻ từ 100 thẻ. \(n\left(\Omega\right)=C_{100}^3\).
Gọi \(x,y,z\) là ba số lấy ra được thỏa mãn.
Biến cố A là biến cố chọn được các số \(x,y,z\) đó.
Đặt \(A_k=\left\{\left(x,y,z\right)|x,y,z\in\left\{1,2,...,100\right\},1\le x< y< z=k,x+y>z\right\}\).
Khi đó \(n\left(A\right)=\left|A_1\right|+\left|A_2\right|+...+\left|A_{100}\right|\). Dễ thấy \(\left|A_1\right|=\left|A_2\right|=\left|A_3\right|=0\).
Ta sẽ tính các giá trị của \(\left|A_k\right|\).
TH1: \(k=2m\).
Xét \(1\le x\le m\). suy ra \(k=2m\ge2x\Leftrightarrow k-x\ge x\)
\(x+y>z\Rightarrow y>k-x\Rightarrow k-x+1\le y\le z-1\)
Số cách chọn \(y\) là \(\left(k-1\right)-\left(k-x+1\right)+1=x-1\) cách.
Xét \(x>m\): \(x+y>2x>2m=z\) (thỏa mãn bđt tam giác)
suy ra \(x+1\le y\le z-1=2m-1\).
Số cách chọn \(y\) là: \(\left(2m-1\right)-\left(x+1\right)+1=2m-x+1\) cách.
Tổng số cách là:
\(\sum\left|A_k\right|=\sum_{i=1}^m\left(i+1\right)+\sum_{i=m+1}^{2m-1}\left(2m-i+1\right)=\left(m-1\right)^2\) cách.
TH2: \(k=2m+1\).
Ta làm tương tự như trên, xét với \(1\le x\le m\) và \(x>m\).
Tổng số cách là: \(\sum\left|A_k\right|=\sum_{i=1}^m\left(i-1\right)+\sum_{i=m+1}^{2m}\left(2m-i\right)=m^2-m\) cách.
Vậy \(n\left(A\right)=\sum_{m=2}^{49}m\left(m-1\right)+\sum_{m=2}^{50}\left(m-1\right)^2=79625\) (cách).
\(P\left(A\right)=\dfrac{n\left(\Omega\right)}{n\left(A\right)}=\dfrac{65}{132}\).

Chọn C
Gọi P là số tiền ông A gửi lúc đầu. Để rút được 100 triệu đồng sau 5 năm ta phải có
P ( 1 + 0 , 068 ) 5 = 100000000
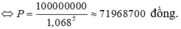
Vì số tiền gửi là tròn triệu đồng nên ông A phải gửi tối thiểu 72 triệu đồng.
Chọn C
Gọi P là số tiền ông A gửi lúc đầu. Để rút được 100 triệu đồng sau 5 năm ta phải có
P ( 1 + 0 , 068 ) 5 = 100000000
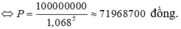
Vì số tiền gửi là tròn triệu đồng nên ông A phải gửi tối thiểu 72 triệu đồng.

Đáp án C
Phương pháp:
Công thức lãi kép, không kỳ hạn: An = M(1 + r%)n
Với: An là số tiền nhận được sau tháng thứ n,
M là số tiền gửi ban đầu,
n là thời gian gửi tiền (tháng),
r là lãi suất định kì (%).
Cách giải:
Số tiền ông A rút ra sau 5 năm đầu là: 100.1 + 8%5 ≈ 146,933 (triệu đồng)
Số tiền ông A tiếp tục gửi là: 146,933:2 ≈ 73,466 (triệu đồng)
Số tiền ông A nhận được sau 5 năm còn lại là: 73,466.1 + 8%5 ≈ 107,946 (triệu đồng)
Sau 10 năm ông A đã thu được số tiền lãi là: 107,946 - 73,466 + 146,933-100 ≈ 81,412 (triệu đồng)