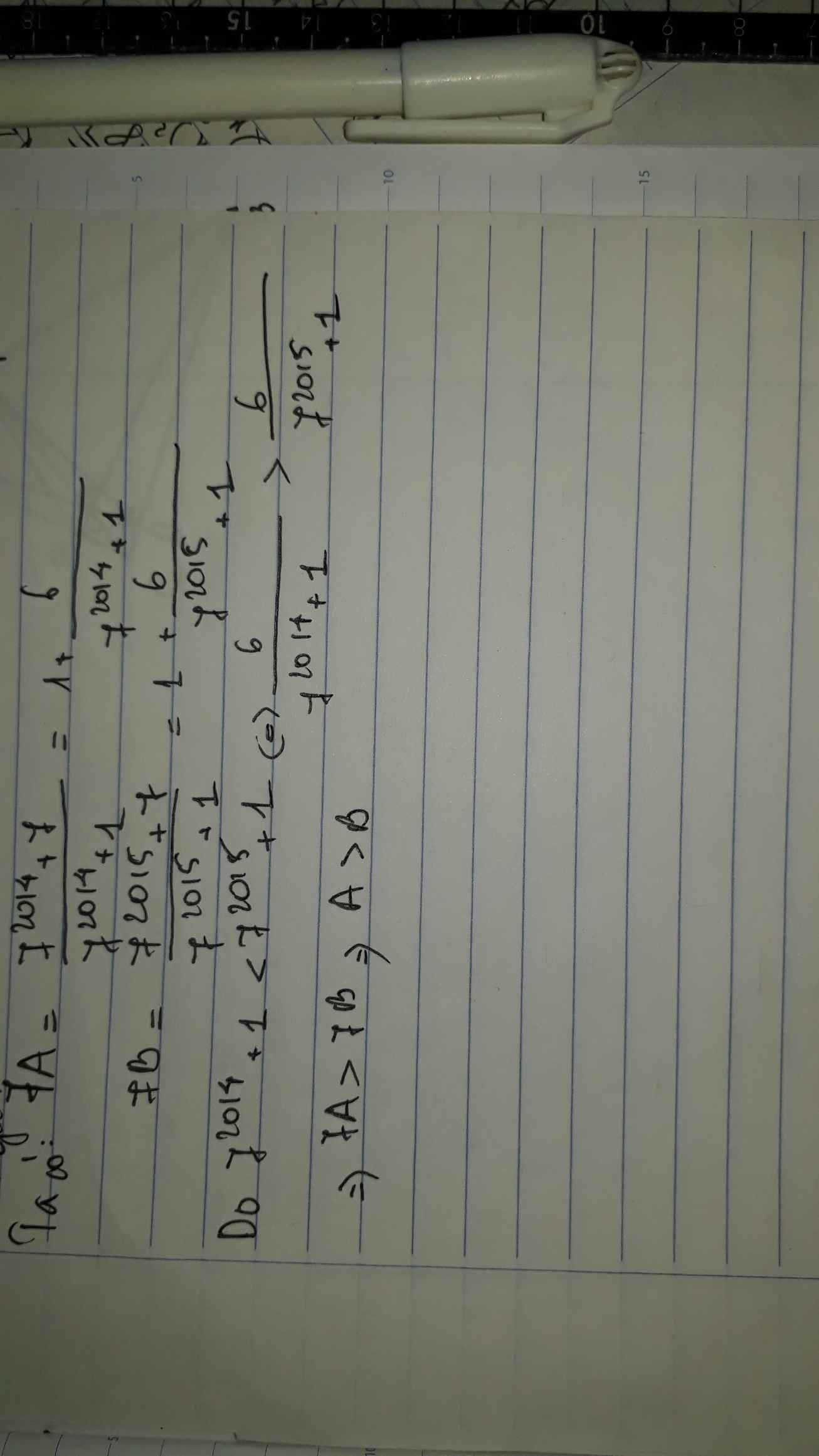Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đặt A= \(\frac{7^{2015}+1}{7^{2017}+1}\)
B= \(\frac{7^{2017}+1}{7^{2019}+1}\)
Ta có A= \(\frac{7^2\left(7^{2015}+1\right)}{7^2\left(7^{2017}+1\right)}\)
= \(\frac{7^{2017}+49}{7^{2019}+49}\)
= \(\frac{7^{2017}+1+48}{7^{2019}+1+48}\)
Vì \(\frac{7^{2017}+1+48}{7^{2019}+1+48}\)>\(\frac{7^{2017}+1}{7^{2019}+1}\)
=> A>B
K MK NHA !
Bạn tham khảo nhé
Ta có công thức :
\(\frac{a}{b}< \frac{a+c}{b+c}\)\(\left(\frac{a}{b}< 1;a,b,c\inℕ^∗\right)\)
Áp dụng vào ta có :
\(B=\frac{7^{2017}+1}{7^{2019}+1}< \frac{7^{2017}+1+48}{7^{2019}+1+48}=\frac{7^{2017}+49}{7^{2019}+49}=\frac{7^2\left(7^{2015}+1\right)}{7^2\left(7^{2017}+1\right)}=\frac{7^{2015}+1}{7^{2017}+1}=B\)
\(\Rightarrow\)\(B< A\) hay \(A>B\)
Vậy \(A>B\)
Chúc bạn học tốt ~

\(TA-CO':\)
\(A=\frac{4+\frac{7}{2014}-\frac{7}{2015}+\frac{7}{2012}-\frac{7}{2013}}{7+\frac{7}{2014}-\frac{7}{2015}+\frac{7}{2012}-\frac{7}{2013}}\)
\(A=\frac{4\left(\frac{1}{2014}-\frac{1}{2015}+\frac{1}{2012}-\frac{1}{2013}\right)}{7\left(\frac{1}{2014}-\frac{1}{2015}+\frac{1}{2012}-\frac{1}{2013}\right)}\)
\(A=\frac{4}{7}\)
\(B=\frac{1+2+...+2^{2013}}{2^{2015}-2}\)
ĐẶT \(C=1+2+...+2^{2013}\)
\(\Rightarrow2C=2+2^2+...+2^{2014}\)
\(\Rightarrow2C-C=\left(2+2^2+...+2^{2014}\right)-\left(1+2+...+2^{2013}\right)\)
\(\Rightarrow C=2^{2014}-2\)
\(\Rightarrow B=\frac{2^{2014}-1}{2^{2015}-2}\)
\(B=\frac{2^{2014}-1}{2\left(2^{2014}-1\right)}\)
\(B=\frac{1}{2}\)
\(\Rightarrow A-B=\frac{3}{7}-\frac{1}{2}=\frac{6}{14}-\frac{7}{14}\)
\(A-B=\frac{6-7}{14}=\frac{-1}{14}\)
VẬY, \(A-B=\frac{-1}{14}\)

\(2.\left(\frac{1}{3}+\frac{1}{5}+\frac{1}{7}+...+\frac{1}{2013}+\frac{1}{2015}+\frac{1}{2017}\right)\)
\(=2.\left(\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+\frac{1}{6}+...+\frac{1}{2017}+\frac{1}{2018}\right)-2.\left(\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+...+\frac{1}{2018}\right)\)
\(=2.\left(\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+\frac{1}{6}+...+\frac{1}{2017}+\frac{1}{2018}\right)-\left(1+\frac{1}{2}+\frac{1}{3}+...+\frac{1}{1009}\right)\)
\(=2.\left(\frac{1}{1010}+\frac{1}{1011}+...+\frac{1}{2018}\right)-1\)

\(A=\frac{2015+2013+2011+...+5+3+1}{2015-2013+2011-2009+...+7-5+3-1}\)
Ta có : 2015 + 2013 + 2011 + ... + 5 + 3 + 1
= [(2015 - 1) : 2 + 1].(2015 + 1) : 2
= 1008.2016 : 2 = 1016064
Lại có : 2015 - 2013 + 2011 - 2009 + ... + 7 - 5 + 3 - 1 (1008 số hạng
= (2015 - 2013) + (2011 - 2009) + ... + (7 - 5) + (3 - 1) (504 cặp)
= 2 + 2 + ... + 2 + 2 (504 số hạng 2)
= 2 x 504 = 1008
Khi đó A = \(\frac{1016064}{1008}=1008\)
b) tTa có : B = \(\frac{1+\frac{1}{3}+\frac{1}{5}+...+\frac{1}{97}+\frac{1}{99}}{\frac{1}{1.99}+\frac{1}{3.97}+\frac{1}{5.95}+...+\frac{1}{97.3}+\frac{1}{99.1}}\)
=> \(\frac{B}{100}\) = \(\frac{1+\frac{1}{3}+\frac{1}{5}+...+\frac{1}{97}+\frac{1}{99}}{\frac{100}{1.99}+\frac{100}{3.97}+\frac{100}{5.95}+...+\frac{100}{97.3}+\frac{100}{99.1}}\)
\(=\frac{1+\frac{1}{3}+\frac{1}{5}+...+\frac{1}{97}+\frac{1}{99}}{1+\frac{1}{99}+\frac{1}{3}+\frac{1}{97}+\frac{1}{5}+\frac{1}{95}+..+\frac{1}{97}+\frac{1}{3}+\frac{1}{99}+1}=\frac{1+\frac{1}{3}+\frac{1}{5}+...+\frac{1}{97}+\frac{1}{99}}{2\left(1+\frac{1}{3}+\frac{1}{5}+...+\frac{1}{97}+\frac{1}{99}\right)}=\frac{1}{2}\)
Khi đó : B/100 = 1/2
=> B = 50
Vậy B = 50

Đặt A= 2015^2013+1/2015^2014+7, B=2015^2014-2/2015^2015-2
2015A= 2015^2014+2015/2015^2014+7= 1 + (2008/2015^2014+7)
2015B= 2015^2015-4030/2015^2015-2= 1 - (4028/2015^2015-2)
Do 2015A>1>2015B nên A>B