
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


224 = (23)8 = 88
316 = (32)8 = 98
Do 8 < 9 nên 88 < 98
--> 224 < 316
Ta có : 224 = 23.8 = (23)8 = 88
316 = 32.8 = (32)8 = 98
Vì 8 < 9 nên 88 < 98
Vậy 224 < 316

Câu 5:
\(2^{24}=8^8\)
\(3^{16}=9^8\)
mà 8<9
nên \(2^{24}< 3^{16}\)
Câu 3 .
\(B=\dfrac{3}{11}.\left(-\dfrac{5}{9}+-\dfrac{13}{18}\right)=\dfrac{3}{11}.-\dfrac{23}{18}=-\dfrac{23}{66}\)

Theo mình :
2335 và 3225
2333<2335 ; 3222<3225
2333=(23)111= 8111
3222= (32)111= 9111
8111<9111
=> 8111<2335<9111<3225
Vậy : 2335 <3225

8^5 = (2^3)^5 = 2^15 = 2^14 . 2
3.4^7 = 3.2^14
2^14 = 2^14 mà 3 > 2 nên 8^5 < 3.4^7
#Đàoo

(-2017)2019 và (-2018)2020
Do số (-2017)2019 có số mũ lẻ nên là số âm
Còn ( -2018)2020 có số mũ chẵn nên là số dương
Ta dễ dàng nhận biết được số âm < số dương
Vậy (-2017)2019 < (-2018)2020
Ta có\(\left(-2017\right)^{2019}=-\left(2017\right)^{2019}< 0\)(1)
\(\left(-2018\right)^{2020}=2018^{2020}>0\)(2)
Từ (1) và (2)\(\Rightarrow\left(-2017\right)^{2019}< \left(-2018\right)^{2020}\)

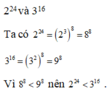

Ta có :
\(2^{24}=\left(2^3\right)^8=8^8\)
\(3^{16}=\left(3^2\right)^8=9^8\)
Vì \(8^8< 9^8\) nên \(2^{24}< 3^{16}\)
Vậy \(2^{24}< 3^{16}\)
Chúc bạn học tốt ~
\(2^{24}=\left(2^3\right)^8=8^8\)
\(3^{16}=\left(3^2\right)^8=9^8\)
Ta có \(8^8< 9^8\)nên \(3^{24}< 3^{16}\)