Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) 32n với 23n
xét 32n: Xét 23n:
=32.3n = 23.2n
=9.3n = 8.2n
Ta thấy: 9>8,3n>2n
=>32n>23n
a , 3^2n và 2^3n
Ta có : 3^2n = 3^2 . n = 9^n
2^3n = 2^3 . n = 8^n
Mà 9^n > 8^n => 3^2n > 2^3n
c , 5^36 và 11^24
Ta có : 5^36 = 5^3 . 12 = 125^12
11^24 = 11^2 . 12 = 121^12
Mà 125^12 > 121^12 => 5^36 > 11^24
b , 5^23 và 6 . 5^22
Ta có : 5^23 = 5 . 5^22
Mà 6 > 5 => 6 . 5^22 > 5 . 5^22
=> 5^23 < 6 . 5^22

- Về phần so sánh hai lũy thừa thi bạn phải làm thế nào cho nó cùng cơ số hoặc cùng số mũ. Sau đó áp dụng quy tắc
Với \(a>b\Rightarrow a^m>b^m\) và ngược lại với a < b (đối với cùng số mũ) hoặc Với \(m>n\Rightarrow a^m>a^n\) và ngược lại với m < n (đối với cùng cơ số)
- Tiếp theo,về dạng: \(A=2+2^2+2^3+...+2^{900}\). Bạn có thấy tất cả cơ số đều là 2 đúng không? Vì chúng ta nhân tất cả cho 2. Được: \(2A=2^2+2^3+2^4+...+2^{901}\)
Sau đó lấy \(2A-A\) được: \(A=2^{901}-2\) (Do 2A - A = A)
Các dạng khác làm tương tự!


Ta có:
\(2^{3^{2^3}}=2^{3^8}=2^{6561}=2^{3.2187}=\left(2^3\right)^{2187}=8^{2187}\)
\(3^{2^{3^2}}=3^{2^9}=3^{512}\)
Vì: 8 > 3 và 2187 > 512
\(\Rightarrow8^{2187}>3^{512}\)
\(\Rightarrow2^{3^{2^3}}>3^{2^{3^2}}\)
Vậy: \(2^{3^{2^3}}>3^{2^{3^2}}\)

32.n=(32)n=9n
23.n=(23)n=8n
Vì: 9n> 8n (9>8; n khác 0)
=> 32.n> 23.n
Ta có: 3^2n=(3^2)^n =9^n
2^3n=(2^3)^n= 8^n
Vì 9^n>8^n nên3^2n>2^3n

=(2.8.16)(a^2.a^3.a^3)(x^2.x^3.x^3)(y,y^4.y^3)
=16^2.a^8.x^8.y^8
=(2^4)^2.(a.x.y)^8
=2^8.(axy)^8
=(2axy)^8

a) 24 và 42.Ta có: b)316 và 275.Ta có:
24=(22)2=42 275=(33)5=315<316
=>24=42.Vậy.. =>275<316.Vậy...
c)233 và 322.Ta có: d)chịu
233=(23)11=811
322=(32)11=911>811.
=>233<322.Vậy....
a) \(2^4\)
\(4^2=\left(2^2\right)^2=2^4\)
\(\Rightarrow2^4=4^2\)
b) \(3^{16}=3^{16}\)
\(27^5=\left(3^3\right)^5=3^{15}\)
\(\Rightarrow3^{16}>27^5\)
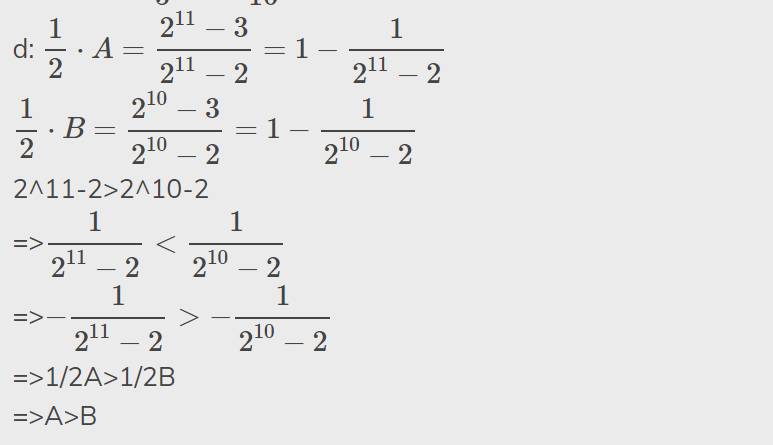
Làm không biết đúng không nha :D
\(2^{3^{2^3}}=\left(\left(2^3\right)^2\right)^3=\left(8^2\right)^3=8^6\)
\(3^{2^{3^2}}=\left(\left(3^2\right)^3\right)^2=\left(9^3\right)^2=9^6\)
\(\Rightarrow\)