OLM cung cấp gói bải giảng điện tử PPT cho giáo viên đầu năm học

Thi thử và xem hướng dẫn giải chi tiết đề tham khảo 12 môn thi Tốt nghiệp THPT 2025

Tập huấn miễn phí ra đề kiểm tra và chấm phiếu trắc nghiệm dành cho giáo viên khối THCS

K
Khách

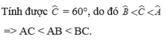
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
Mua vip
NT
nguyen thi luong
26 tháng 2 2015 - olm

Cho tam giác ABC có góc A =80 độ,gócC=40 độ 

a,hãy so sánh các cạnh của tam giác đó.

b,hãy cho biết tam giác đó là tam giác gì?
#Toán lớp 7
0
SG
Sách Giáo Khoa
11 tháng 5 2017

So sánh các cạnh của tam giác ABC biết \(\widehat{A}=80^0,\widehat{C}=40^0\) ?
#Toán lớp 7
1
G
Giang
6 tháng 2 2018

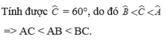
Giải:

Ta có: \(\widehat{A}=80^0\)

\(\widehat{C}=40^0\)

\(\Leftrightarrow\widehat{B}=180^0-80^0-40^0=60^0\) (Tổng ba góc của một tam giác)

Suy ra: \(\widehat{A}>\widehat{B}>\widehat{C}\)

\(\Leftrightarrow BC>AC>AB\) (Tính chất giữa góc và cạnh đối diện)

Vậy ...

Đúng(0)
AT
Anh Triêt
6 tháng 2 2018

sachbaitap.com

Đúng(0)
VP
Vampire Princess
22 tháng 3 2018 - olm

So sánh các cạnh của tam giác ABC, biết rằng: góc A = 80 độ ,góc B = 45 độ
#Toán lớp 7
3
ON
Oh Nova
22 tháng 3 2018

AC<BC Vì góc A > góc B(80>45)

Đúng(0)
SO
say oh noo
22 tháng 3 2018

goc A > goc C > goc B dung bam dung cho nhe 

Đúng(0)
PN
Phương Nghi
15 tháng 4 2020 - olm
1)So sánh các cạnh của Tam giác ABC biết A= 80° B=40°2)Sosánh các cạnh của Tam giác PQR biết P = 70° R= 50°3) Cho tam giác ABC vuông tại A , điểm K nằm giữa A và C . So sánh độ dài BK và BC 4) cho tam giác MNP vuông tại N . Trên tia đối của tia PN lấy điểm Q . So sánh độ dài MP và MQ5) Cho tam giác ABC có ba góc nhọn AB < AC . Kẻ BD vuông góc với AC tại D , CD vuông góc với AB tại E . Gọi H là giao điểm của...
Đọc tiếp

1)So sánh các cạnh của Tam giác ABC biết A= 80° B=40°

2)Sosánh các cạnh của Tam giác PQR biết P = 70° R= 50°

3) Cho tam giác ABC vuông tại A , điểm K nằm giữa A và C . So sánh độ dài BK và BC 

4) cho tam giác MNP vuông tại N . Trên tia đối của tia PN lấy điểm Q . So sánh độ dài MP và MQ

5) Cho tam giác ABC có ba góc nhọn AB < AC . Kẻ BD vuông góc với AC tại D , CD vuông góc với AB tại E . Gọi H là giao điểm của BC và CE . So sánh độ dài của HB và HC

 
#Toán lớp 7
0
PH
Phan Hoàng Quyên
25 tháng 11 2021

Cho tam giác ABC có A=2B và B+C=80 độ. Hãy so sánh các cạnh của tam giác ABC.
#Toán lớp 7
0
CN
chi nguyễn
30 tháng 1 2023

cho tam giác abc có góc a bằng 60 độ b bằng 80 độ .vẽ tia phân giác AD của góc A (AD cắt BC tại D) a) tính góc ADB b)so sánh các cạnh của tam giác ABD c)so sánh các cạnh của tam giác ADC
#Toán lớp 7
2
NL
Nguyễn Lê Phước Thịnh
30 tháng 1 2023

a: góc C=180-60-80=40 độ

góc BAD=góc CAD=60/2=30 độ

góc ADB=180-80-30=70 độ

b: vì góc BAD<góc ADB<góc ABD

nên BD<AB<AD

c: góc ADC=180-70=110 độ

Vì góc ADC>góc C>góc DAC

nên AC>AD>CD

Đúng(0)
NV
Nhật Văn
30 tháng 1 2023

a) Góc C = 180 - 60 - 80 = 400

Góc BAD = góc CAD = \(\dfrac{60}{2}\) = 300

Góc ADB = 180 - 80 - 30 = 700

b) Vì góc BAD < góc ADB < góc ABD

nên BD < AB < AD

c) Góc ADC = 180 - 70 = 1100

Vì góc ADC > góc C > góc DAC

nên AC > AD > CD

Đúng(0)
CC
công chúa xinh xắn
3 tháng 9 2016 - olm

So sánh các cạnh của tam giác ABC ,biết rằng : góc A =800 ; góc B = 450
#Toán lớp 7
5
LM
Lê Minh Anh
3 tháng 9 2016

Trong tam giác ABC có: \(\widehat{A}+\widehat{B}+\widehat{C}=180\Rightarrow80+45+\widehat{C}=180\Rightarrow125+\widehat{C}=180\Rightarrow\widehat{C}=55\)

Ta có: \(\widehat{A}>\widehat{B}\left(80>45\right)\Rightarrow BC>AC\)(1)

\(\widehat{A}>\widehat{C}\left(80>55\right)\Rightarrow BC>AB\)           (2)

\(\widehat{C}>\widehat{B}\left(55>45\right)\Rightarrow AB>AC\)           (3)

Từ (1);(2);(3) ta có: BC > AB > AC

(Mình không biết ghi kí hiệu độ nên bạn chịu khó để ý rồi thêm vào bài làm nha)

Đúng(1)
MA
Minh Anh
3 tháng 9 2016

Có: Góc A=800 ; Góc B=450

=> Góc C = 1800 - 800  - 450 = 550

Vì: 450 < 550 < 800

Vậy: Góc B < Góc C < Góc A

Đúng(0)
TH
Trần Hạnh Nguyên
5 tháng 3 2021

so sánh các cạnh của tam giác abc biết b= 40 độ c= 60 độ 

 
#Toán lớp 7
2
A
︵✰Ah
5 tháng 3 2021

 

so sánh các cạnh của tam giác abc biết b= 40 độ c= 60 độ 

Góc A> Góc C>Góc B

 

Đúng(1)
S
✟şin❖
5 tháng 3 2021

AC < AB <BC

Đúng(5)
SH
Sheep Habt
30 tháng 4 2022

Câu 17. Cho tam giác ABC vuông tại A có B=40°. So sánh các cạnh của tam giác ABC.
#Toán lớp 7
1
C
Chuu
30 tháng 4 2022

Ta có :

góc A + góc  B + góc C  = 1800

hay 900 + 400 + góc C = 1800

C = 180 - ( 90 +40)

góc C = 500

Trong △ABC vuông tại A có

góc A > góc C > góc B 

hay BC > AB > AC

Đúng(3)
Bảng xếp hạng
Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
  • Tuần
  • Tháng
  • Năm
Các khóa học có thể bạn quan tâm
Tổng thanh toán: 0đ (Tiết kiệm: 0đ)
Tới giỏ hàng
Yêu cầu VIP