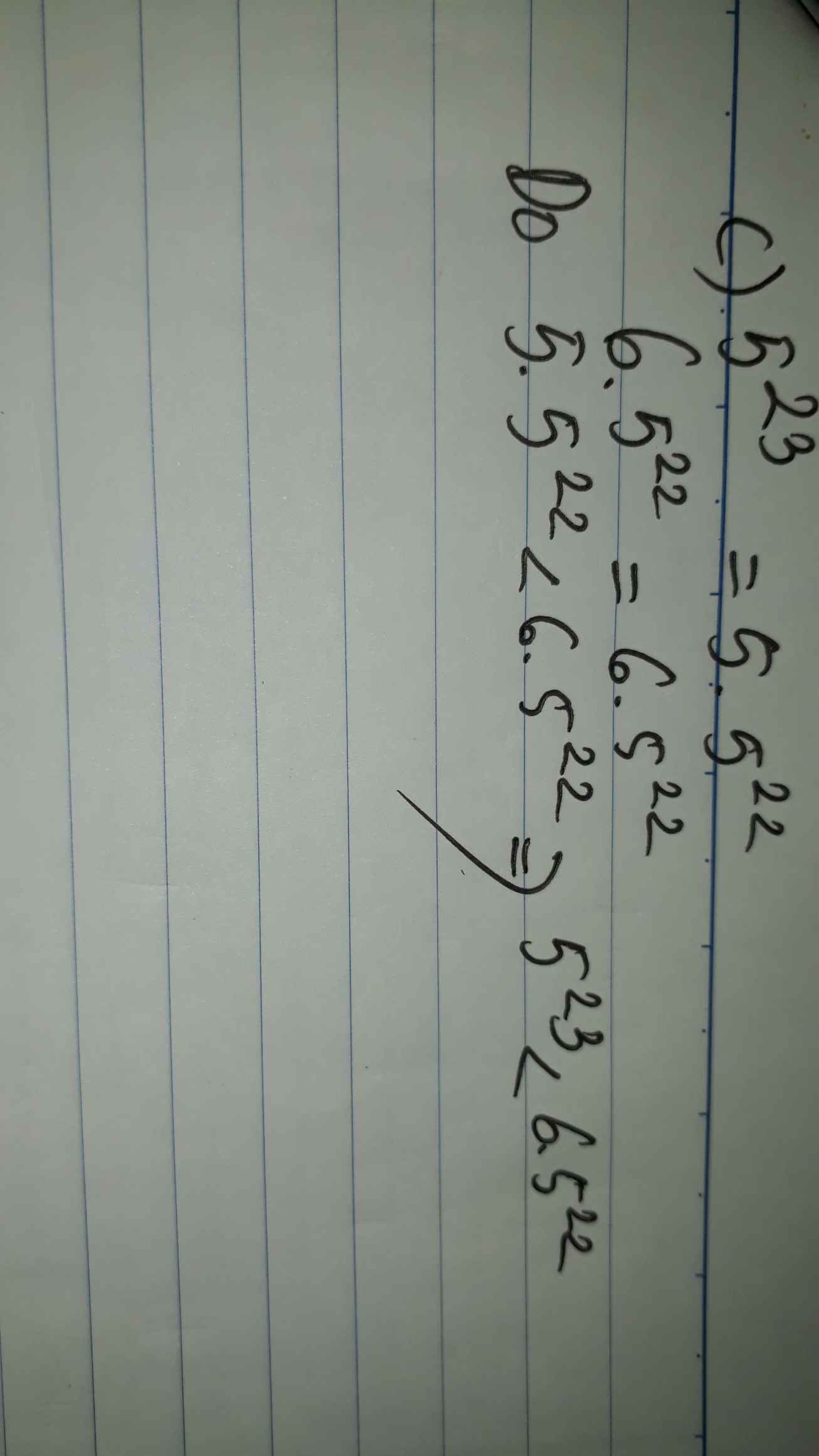K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
3 tháng 10 2021
27 mũ 11 và 81 mũ 8
625 mũ 5 và 125 mũ 7
5 mũ 36 và 11 mũ 24
5 mũ 23 và 6,5 mũ 22
7.2 mũ 13 và 2 mũ 16
HA
1
31 tháng 8 2024
11 mũ 39 > 5 mũ 26 vì cơ số và số mũ đều hơn
2 mũ 125 và 3 mũ 75
2^125=(2^5)^25=32^25
3^75=(3^3)^25=27^25
Vì 32^25>27^25 nên 2^125>3^75
5^40=(5^4)^10=3125^10
Vì 3125^10>620^10 nên 5^40>620^10
MD
12 tháng 11 2017
a,5mũ 36=(5mũ3)mũ12=125 mũ12
11^24=(11^2)12=121^12
vì 121<125 nên 5^36>11^24
GC
3
23 tháng 8 2017
a)Ta có:\(5^{36}=\left(5^3\right)^{12}=125^{12}\)
\(11^{24}=\left(11^2\right)^{12}=121^{12}\)
Vì \(125^{12}>121^{12}\)\(\Rightarrow5^{36}>11^{24}\)
H
1
3 tháng 10 2018
5^36=(5^3)^12 = 125^12
11^24 =( 11^2 ) ^12 = 121^12
do 125^12>121^12 nên 5^36 > 11^24
câu cò lại tương tự
1 tháng 8 2015
1/ a) \(2.3.12.12.3=2.3.2^2.3.2^2.3.3=2^5.3^4\)
b) \(3.5.27.125=3.5.3^3.5^3=3^4.5^4=\left(3.5\right)^4\)
2/ a) \(\left(27^3\right)^4=27^{3.4}=27^{12}\)
Vậy \(\left(27^3\right)^4=27^{12}\)
b) \(5^{36}=\left(5^6\right)^6\) và \(11^{24}=\left(11^4\right)^6\)
Do đó \(5^6=15625\) và \(11^4=14641\)
Vì 15625>14641 nên\(\left(5^6\right)^6>\left(11^4\right)^6hay5^{36}>11^{24}.\)
3/ a) \(x^3=125=>x=5\)
b) \(\left(3x-14\right)^3=2^5.5^2+200\)
\(\left(3x-14\right)^3=1000\)
\(3x-14=10^3\)
\(3x=10^3+14\)
\(3x=1014\)
\(x=\frac{1014}{3}=338\)
c) \(\left(2x-1\right)^4=81\)
\(\left(2x-1\right)^4=3^4\)
\(2x-1=3\)
\(2x=3+1\)
\(x=\frac{4}{2}=2\)
d) \(5x+3^4=2^2.7^2\)
\(5x+3^4=\left(2.7\right)^2=14^2\)
\(5x+81=196\)
\(5x=196-81\)
\(5x=115\)
\(x=\frac{115}{5}=23\)
e) \(4^x=1024=>x=5\).
SN
12 tháng 10 2018
a,
15^12=(3*5)^12=3^12*5^12
81^3*125^5=(3^4)^3*(5^3)^5=3^12*5^15
Vì 12<15 suy ra 5^12<5^15
Suy ra 3^12*5^12<3^12*5^15
T
12 tháng 10 2018
\(a.81^3.125^5=\left(3^4\right)^3.\left(5^3\right)^5=3^{12}.5^{15}=3^{12}.5^{12}.5^3=\left(3.5\right)^{12}.5^3=15^{12}.5^3>15^{12}\)
\(b.4^{20}.81^{12}=\left(2^2\right)^{20}.\left(9^2\right)^{12}=2^{40}.9^{24}=2^{20}.2^{20}.9^{20}.9^4=\left(2.9\right)^{20}.2^{20}.9^4=18^{20}.2^{20}.9^4>18^{20}\)
\(c.73^{75}=\left(73^3\right)^{25}=389017^{25}\)
\(107^{50}=107^{2.50}=\left(107^2\right)^{25}=11449^{25}\)
Vì \(389017^{25}>11449^{25}\Rightarrow73^{75}>107^{50}\)
