
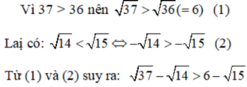
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

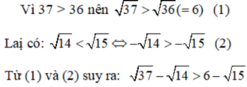

Ta có \(6=\sqrt{36}\)
\(\sqrt{37}-\sqrt{14}=\sqrt{37}+\left(-\sqrt{14}\right)\)
\(6-\sqrt{15}=\sqrt{36}-\sqrt{15}=\sqrt{36}+\left(-\sqrt{15}\right)\)
Vì \(\sqrt{37}>\sqrt{36}\) và \(-\sqrt{14}>-\sqrt{15}\)
\(\Rightarrow\sqrt{37}+\left(-\sqrt{14}\right)>\sqrt{36}+\left(-\sqrt{15}\right)\)
\(\Rightarrow\sqrt{37}-\sqrt{14}>\sqrt{36}-\sqrt{15}\)
hay \(\sqrt{37}-\sqrt{14}>6-\sqrt{15}\)
Chúc bn học tốt ![]()
![]()
![]()
![]()
![]()

a) Ta có: 2002/2003 < 1 (1)
14/13 > 1 (2)
Từ (1) và (2) => 2002/2003 < 14/13

a: \(\left(\sqrt{21}-\sqrt{5}\right)^2=26-2\sqrt{105}\)
\(\left(\sqrt{20}-\sqrt{6}\right)^2=26-2\sqrt{120}\)
mà \(-2\sqrt{105}>-2\sqrt{120}\)
nên \(\sqrt{21}-\sqrt{5}>\sqrt{20}-\sqrt{6}\)
b: \(\left(\sqrt{2}+\sqrt{8}\right)^2=10+2\cdot4=16=12+4\)
\(\left(3+\sqrt{3}\right)^2=12+6\sqrt{3}\)
mà \(4< 6\sqrt{3}\)
nên \(\sqrt{2}+\sqrt{8}< 3+\sqrt{3}\)

c) Đặt \(A=2^0+2^1+2^2+...+2^{50}\)
\(\Leftrightarrow2A=2^1+2^2+2^3...+2^{51}\)
\(\Leftrightarrow2A-A=2^1+2^2+2^3...+2^{51}\)\(-2^0-2^1-2^2-...-2^{50}\)
\(\Leftrightarrow A=2^{51}-2^0=2^{51}-1< 2^{51}\)
Vậy \(2^0+2^1+2^2+...+2^{50}< 2^{51}\)
a)Ta có: \(\hept{\begin{cases}2^{30}=\left(2^3\right)^{10}=8^{10}\\3^{30}=\left(3^3\right)^{10}=27^{10}\\4^{30}=\left(2^2\right)^{30}=2^{60}\end{cases}}\)và \(\hept{\begin{cases}3^{20}=\left(3^2\right)^{10}=9^{10}\\6^{20}=\left(6^2\right)^{10}=36^{10}\\8^{20}=\left(2^3\right)^{20}=2^{60}\end{cases}}\)
Mà \(8^{10}< 9^{10}\); \(27^{10}< 36^{10}\);\(2^{60}=2^{60}\)nên
\(8^{10}+27^{10}+2^{60}< 9^{10}+36^{10}+2^{60}\)
hay \(2^{30}+3^{30}+4^{30}< 3^{20}+6^{20}+8^{20}\)

\(2^{27}=2^{3.9}=8^9\)
\(3^{18}=3^{2.9}=9^9\)
Vì \(9^9>8^9\Rightarrow3^{18}>2^{27}\)
MK chỉ làm đc câu a) thui nha :
2^27 = 2^ 3.9 = 8^9
3^18 = 3^2.9=9^9
Vì 9^9 > 8^9 => 2^27 < 2 ^18

d) 812 và 128
Ta có : 812 = (96)2 = 5314412
128 = (124)2 = 207362
=> 534412 > 207362
=> 812 > 128
a) 36 và 63
Ta có : 36 = (32)3 = 93
63 = 63
=> 93 > 63
=> 36 > 63