
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1:
a: -8/12<0<-3/-4
b: -56/24<0<7/3
c: 4/25<1<15/13
=>-4/25>-15/13
Bài 2:
a: =-60/45=-4/3
b: =4/15-3/2-8/5=8/30-45/30-48/30=-85/30=-17/6

1,-(4+7)=(-4-7)
2,-(12-25)=(-12+25)
3,-(-8+7)=(8-7)
4,+(-15-4)=(-15-4)
5,+(23-12)=(23-12).

\(-\dfrac{4}{5};\dfrac{6}{7}\)
Có \(MSC=35\)
\(-\dfrac{4}{5}=\dfrac{-4\times7}{5\times7}=-\dfrac{28}{35}\)
\(\dfrac{6}{7}=\dfrac{6\times5}{7\times5}=\dfrac{30}{35}\)
So sánh :
\(-\dfrac{3}{7}=-0,43;\dfrac{4}{-9}=-0,44;\dfrac{25}{-15}=-1,66\)
\(\Rightarrow\dfrac{25}{-15}>\dfrac{4}{-9}>-\dfrac{3}{7}\)


A=1/5 + 1/15 + 1/25 + 1/35 + 1/65 + 1/75 + 1/85
Tính tổng A và so sánh A với 1/2. Đề như thế à?

b, TH 1: \(a>5\Rightarrow a-5>0\Rightarrow35\cdot\left(a-5\right)>31\cdot\left(a-5\right)\)
TH 2: \(a<5\Rightarrow a-5<0\Rightarrow35\cdot\left(a-5\right)<31\cdot\left(a-5\right)\)
TH 3: \(a=5\Rightarrow a-5=0\Rightarrow35\cdot\left(a-5\right)=31\cdot\left(a-5\right)=0\)

Theo phương pháp so sánh hai phân số có cùng mẫu số mà chúng ta đã được học thì bạn Liên giải thích đúng, còn Oanh giải thích sai.
Ví dụ cho thấy bạn Oanh sai : hai phân số 3/8 và 1/2 có 3 lớn hơn 1 còn 8 lớn hơn 2 nhưng 3/8 nhỏ hơn 1/2 vì khi quy đồng về mẫu số chung là 8 thì ta có: 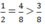

a, \(125^{20}\)và \(25^{30}\)
ta có : \(125^{20}=\left(5^3\right)^{20}\)\(=5^{3.20}=5^{60}\)
\(25^{30}=\left(5^2\right)^{30}=5^{2.30}=5^{60}\)
Vì \(5^{60}=5^{60}\)nên => \(125^{20}=25^{30}\)
b ,\(49^{16}\)và \(343^{20}\)
ta có : \(49^{16}=\left(7^2\right)^{16}=7^{2.16}=7^{32}\)
\(343^{20}=\left(7^3\right)^{20}=7^{3.20}=7^{60}\)
Vì \(7^{32}< 7^{60}\)nên => \(49^{16}< 343^{20}\)
c, \(121^{15}\)và \(1331^{16}\)
ta có : \(121^{15}=\left(11^2\right)^{15}=11^{2.15}=11^{30}\)
\(1331^{16}=\left(11^3\right)^{16}=11^{3.16}=11^{48}\)
Vì \(11^{30}< 11^{48}\)nên => \(121^{15}< 1331^{16}\)
d, \(199^{20}\)và \(2003^{15}\)
ta có : \(199^{20}=199^{5.4}=\left(199^4\right)^5=1568239201^5\)
\(2003^{15}=2003^{3.5}=\left(2003^3\right)^5=8036054027^5\)
Vì \(1568239201^5< 8036054027^5\)nên => \(199^{20}< 2003^{15}\)
e, \(4^{25}\)và \(3^{30}\)
=> \(4^{25}< 3^{30}\)
f, \(36^{82}\)và \(49^{123}\)
=> \(36^{82}< 49^{123}\)
mình làm rồi đó . k mình đi