A
5
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
LT
2
27 tháng 1 2023
\(A=\dfrac{10^{12}+6}{10^{12}-11}\)
\(\Rightarrow A=\dfrac{10^{12}-11+17}{10^{12}-11}\)
\(\Rightarrow A=\dfrac{10^{12}-11}{10^{12}-11}+\dfrac{17}{10^{12}-11}\)
\(\Rightarrow A=1-\dfrac{17}{10^{12}-11}\)
\(B=\dfrac{10^{11}+5}{10^{11}-12}\)
\(\Rightarrow B=\dfrac{10^{11}-12+17}{10^{11}-12}\)
\(\Rightarrow B=\dfrac{10^{11}-12}{10^{11}-12}+\dfrac{17}{10^{11}-12}\)
\(\Rightarrow B=1-\dfrac{17}{10^{11}-12}\)
Vậy ta cần so sánh \(1-\dfrac{17}{10^{12}-11}\) và \(1-\dfrac{17}{10^{11}-12}\)
Ta thấy \(\left(10^{12}-11\right)>\left(10^{11}-12\right)\) và 2 phân số trên cùng tử số 17 nên \(\dfrac{17}{10^{12}-11}< \dfrac{17}{10^{11}-12}\)
Vậy \(1-\dfrac{17}{10^{12}-11}>1-\dfrac{17}{10^{11}-12}\) hay \(A>B\)
AH
Akai Haruma
Giáo viên
7 tháng 12 2023
Lời giải:
a.
\(\frac{n+1}{n+2}=\frac{n+1}{n+2}+1-1=\frac{2n+3}{n+2}-1\)
\(> \frac{2n+3}{n+3}-1=\frac{(n+3)+n}{n+3}-1=\frac{n}{n+3}\)
b.
\(10A=\frac{10^{12}-10}{10^{12}-1}=\frac{(10^{12}-1)-9}{10^{12}-1}=1-\frac{9}{10^{12}-1}<1\)
\(10B=\frac{10^{11}+10}{10^{11}+1}=\frac{(10^{11}+1)+9}{10^{11}+1}=1+\frac{9}{10^{11}+1}>1\)
$\Rightarrow 10A< 10B\Rightarrow A< B$
LT
1
19 tháng 2 2016
a) Có (-11).(-12) = 132
10.(-13)= -130
Mà 132> -130
Suy ra (-11).(-12) > 10.(-13)
b) giống với câu a
24 tháng 2 2018
Anh cũng nằm trong đội tuyển nàk em tham khảo nhé
Ta có :
\(A=\frac{10^{11}-1}{10^{12}-1}\)
\(\Leftrightarrow\)\(10A=\frac{10^{12}-10}{10^{12}-1}=\frac{10^{12}-1}{10^{12}-1}-\frac{9}{10^{12}-1}=1-\frac{9}{10^{12}-1}< 1\)\(\left(1\right)\)
Lại có :
\(B=\frac{10^{10}+1}{10^{11}+1}\)
\(\Leftrightarrow\)\(10B=\frac{10^{11}+10}{10^{11}+1}=\frac{10^{11}+1}{10^{11}+1}+\frac{9}{10^{11}+1}=1+\frac{9}{10^{11}+1}>1\)\(\left(2\right)\)
Từ (1) và (2) suy ra \(10A< 1< 10B\) hay \(A< B\)
Vậy \(A< B\)
24 tháng 2 2018
10A=\(\frac{10^{12}-10}{10^{12}-1}\)=\(1-\frac{9}{10^{12}-1}\)
10B=\(\frac{10^{11}+10}{10^{11}+1}=1+\frac{9}{10^{11}+1}\)
Sao sánh 10A với 10B
Vì 1=1 nên so sánh \(-\frac{9}{10^{12}-1}\)với \(\frac{9}{10^{11}+1}\)
=> \(-\frac{9}{10^{12}-1}< \frac{9}{10^{11}+1}\)
=> 10A < 10B
=> A < B
NN
0
NK
3
YN
9 tháng 2 2023
\(A=\dfrac{10^{11}+1}{10^{12}-1}\)
\(\Rightarrow10A=\dfrac{10^{11}+1}{10^{12}-1}.10\)
\(\Rightarrow10A=\dfrac{10\left(10^{11}+1\right)}{10^{12}-1}\)
\(\Rightarrow10A=\dfrac{10^{12}-10}{10^{12}-1}\)
\(B=\dfrac{10^{10}+1}{10^{11}+1}\)
\(\Rightarrow10B=\dfrac{10^{10}+1}{10^{11}+1}.10\)
\(\Rightarrow10B=\dfrac{\left(10^{10}+1\right).10}{10^{11}+1}\)
\(\Rightarrow10B=\dfrac{10^{11}+10}{10^{11}+1}\)
Ta thấy:
\(10^{12}-1>10^{12}-10>0\Rightarrow10A< 1\)
\(0< 10^{11}+1< 10^{11}+10\Rightarrow10B>1\)
Mà \(10A< 1;10B>1\)
\(\Rightarrow B>A\).
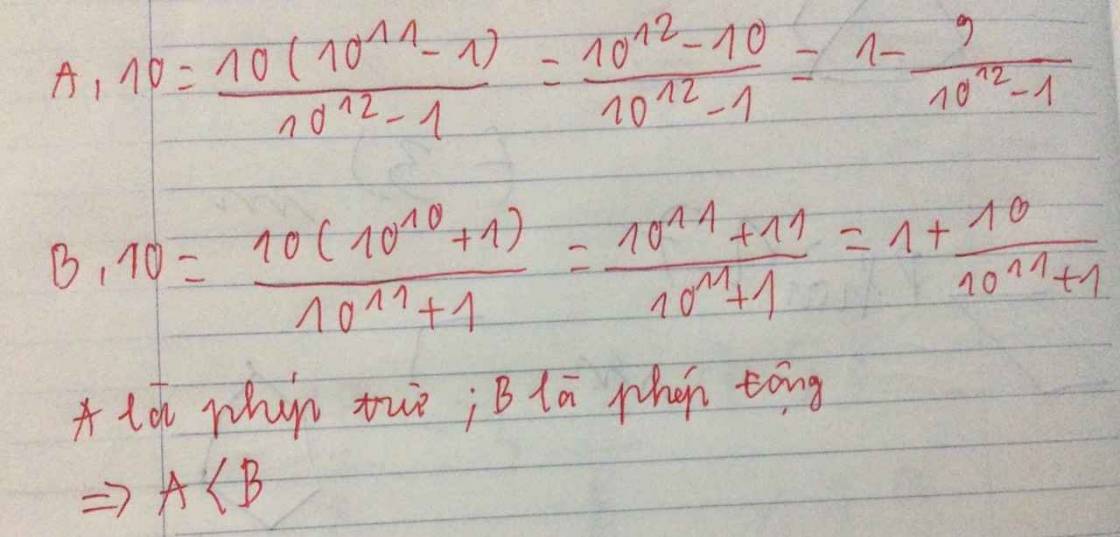
Ta có :
\(\frac{10}{11}>\frac{10}{11+12};\frac{11}{12}>\frac{11}{11+12}\)
\(\Rightarrow\frac{10}{11}+\frac{11}{12}>\frac{10}{11+12}+\frac{11}{11+12}\)
\(\Rightarrow\frac{10}{11}+\frac{11}{12}>\frac{10+11}{11+12}\)
Vậy \(\frac{10}{11}+\frac{11}{12}>\frac{10+11}{11+12}\)
Chúc bạn học tốt !!!
ta có: \(\frac{10+11}{11+12}=\frac{10}{11+12}+\frac{11}{11+12}\)
mà \(\frac{10}{11}>\frac{10}{11+12}\)
\(\frac{11}{12}>\frac{11}{11+12}\)
\(\Rightarrow\frac{10}{11}+\frac{11}{12}>\frac{10}{11+12}+\frac{11}{11+12}\)
\(\Rightarrow\frac{10}{11}+\frac{11}{12}>\frac{10+11}{11+12}\)