NH
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
22 tháng 1 2015
Bài này hay thật mình thì chỉ nghĩ ra mỗi cách này. Nhưng ko biết vs học phô thông thì tư duy thế nào
1 số chính phương có tận cùng bằng 0,1,4,5,6,9
N+1 tận cùng =9=> n tận cùng bằng 8 => 2n+1 tận cùng =7 => loại
(2n+1)-(n+1)=n=a^2-b^2=(a-b)(a+b)
2n+1 là số lẻ => a lẻ
N chẵn=> b chẵn
1 số chính phương chia cho 4 dư 0 hoặc 1 => (a+b)(a-b) chia hết cho 8
Còn nó chia hết cho 3 hay không thì phải dùng định lý của fermat đẻ giải
http://en.wikipedia.org/wiki/Fermat%27s_little_theorem
như vậy chưng minh no chia het cho 8 và 3 là có thể két luạn nó chia hêt cho 24
LP
1
4 tháng 9 2016
Ta có: (2n+1) chia hết cho(n+2)
=> 2n + 4 - 3 chia hết cho n + 2
=> 2.(n + 2) - 3 chia hết cho n + 2
=> 3 chia hetes cho n + 2
=> n + 2 thuộc Ư(3) = {-1;1-3;3}
Ta có:
| n + 2 | -3 | -1 | 1 | 3 |
| n | -5 | -3 | -1 | 1 |
Vì là giá trị nhỏ nhất nên n = -5
TN
0
ND
Nguyễn Đức Trí
VIP
30 tháng 7 2023
Ta có :
\(10\le n\le99\)
\(\Rightarrow21\le2n+1\le201\)
\(\Rightarrow2n+1\) là số chính phương lẻ (1)
\(\Rightarrow2n+1\in\left\{25;49;81;121;169\right\}\)
\(\Rightarrow n\in\left\{12;24;40;60;84\right\}\)
\(\Rightarrow3n+1\in\left\{37;73;121;181;253\right\}\left(2\right)\)
\(\left(1\right),\left(2\right)\Rightarrow\dfrac{2n+1}{3n+1}=\dfrac{2.40+1}{3.40+1}=\dfrac{81}{121}=\left(\dfrac{9}{11}\right)^2\left(n=40\right)\)
\(\Rightarrow dpcm\)
\(\Rightarrow n=40⋮40\Rightarrow dpcm\)
LV
0
QA
1
12 tháng 11 2021
ĐKXĐ: \(x\ne-1\)
\(X=\dfrac{2n+10}{n+1}=\dfrac{2\left(n+1\right)+8}{n+1}=2+\dfrac{8}{n+1}\in Z\)
\(\Rightarrow\left(n+1\right)\inƯ\left(8\right)=\left\{-8;-4;-2;-1;1;2;4;8\right\}\)
Kết hợp ĐKXĐ:
\(\Rightarrow n\in\left\{-9;-5;-3;-2;0;1;3;7\right\}\)
18 tháng 3 2018
Vì 2n+1 là số chính phương lẻ nên
2n+1≡1(mod8)⇒2n⋮8⇒n⋮42n+1≡1(mod8)⇒2n⋮8⇒n⋮4
Do đó n+1 cũng là số lẻ, suy ra
n+1≡1(mod8)⇒n⋮8n+1≡1(mod8)⇒n⋮8
Lại có
(n+1)+(2n+1)=3n+2(n+1)+(2n+1)=3n+2
Ta thấy
3n+2≡2(mod3)3n+2≡2(mod3)
Suy ra
(n+1)+(2n+1)≡2(mod3)(n+1)+(2n+1)≡2(mod3)
Mà n+1 và 2n+1 là các số chính phương lẻ nên
n+1≡2n+1≡1(mod3)n+1≡2n+1≡1(mod3)
Do đó
n⋮3n⋮3
Vậy ta có đpcm.
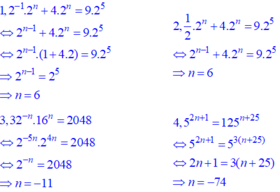
pn ay lừa pn đó pn do ko trả loi dau
\(\frac{1}{2}\cdot2^n+4.2^n=9.2^5\)
\(2^n\left(\frac{1}{2}+4\right)=9.32\)
\(2^n\left(\frac{1}{2}+\frac{8}{2}\right)=288\)
\(2^n\cdot\frac{9}{2}=288\)
\(2^n=288:\frac{9}{2}\)
\(2^n=288\cdot\frac{2}{9}\)
\(2^n=64\)
\(2^n=2^6\)
=> n = 6
vậy n = 6