

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



gợi ý: a)chia 2 vế cho căn 5
đặt \(\frac{1}{\sqrt{5}}=cosa\Rightarrow\frac{2}{\sqrt{5}}=sina\)
khi đó pt <=>sin(x-a)=\(\frac{3}{\sqrt{5}}>1\)
->vô nghiệm
bn giải thích cho mk chỗ này được ko : \(\frac{1}{\sqrt{5}}=\cos a\Rightarrow\frac{2}{\sqrt{5}}=\sin a\)

1/ \(cosx=\frac{1}{3}\Rightarrow x=\pm a+k2\pi\) với \(cosa=\frac{1}{3}\)
Tổng các nghiệm:
\(\sum x=a+a+2\pi+\left(-a+2\pi\right)+\left(-a+4\pi\right)=8\pi\)
2/ ĐKXĐ:...
\(\Leftrightarrow1+tan^2x-2tanx-4=0\)
\(\Leftrightarrow tan^2x-2tanx-3=0\)
\(\Rightarrow\left[{}\begin{matrix}tanx=-1\\tanx=3\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=-\frac{\pi}{4}+k\pi\\x=arctan3+k\pi\end{matrix}\right.\)
b/ Không hiểu đề đoạn này \(sinx.cosx\left(x+\frac{\pi}{2}\right)\) , góc trong ngoặc không biết là của cái gì?
c/ ĐKXĐ:...
\(1+cot^2x+3tan^2x=5\)
\(\Leftrightarrow\frac{1}{tan^2x}+3tan^2x-4=0\)
\(\Leftrightarrow3tan^4x-4tan^2x+1=0\)
\(\Rightarrow\left[{}\begin{matrix}tan^2x=1\\tan^2x=\frac{1}{3}\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}tanx=\pm1\\tanx=\pm\frac{1}{\sqrt{3}}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\pm\frac{\pi}{4}+k\pi\\x=\pm\frac{\pi}{6}+k\pi\end{matrix}\right.\)
d/
ĐKXĐ: \(sinx\ne0\Rightarrow cosx\ne\pm1\)
\(2.cos^2x=1-cosx\)
\(\Leftrightarrow2cos^2x+cosx-1=0\)
\(\Rightarrow\left[{}\begin{matrix}cosx=-1\left(l\right)\\cosx=\frac{1}{2}\end{matrix}\right.\)
\(\Rightarrow cosx=cos\frac{\pi}{3}\)
\(\Rightarrow\left[{}\begin{matrix}x=\frac{\pi}{3}+k2\pi\\x=-\frac{\pi}{3}+k2\pi\end{matrix}\right.\)

a) Đặt t = cos![]() , t ∈ [-1 ; 1] thì phương trình trở thành
, t ∈ [-1 ; 1] thì phương trình trở thành
(1 - t2) - 2t + 2 = 0 ⇔ t2 + 2t -3 = 0 ⇔ ![]()
Phương trình đã cho tương đương với
cos![]() = 1 ⇔
= 1 ⇔ ![]() = k2π ⇔ x = 4kπ, k ∈ Z.
= k2π ⇔ x = 4kπ, k ∈ Z.
b) Đặt t = sinx, t ∈ [-1 ; 1] thì phương trình trở thành
8(1 - t2) + 2t - 7 = 0 ⇔ 8t2 - 2t - 1 = 0 ⇔ t ∈ {![]() }.
}.
Các nghiệm của phương trình đã cho là nghiệm của hai phương trình sau :
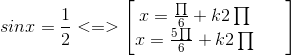
và ![]()
Đáp số : x = ![]() + k2π; x =
+ k2π; x = ![]() + k2π;
+ k2π;
x = arcsin(![]() ) + k2π; x = π - arcsin(
) + k2π; x = π - arcsin(![]() ) + k2π, k ∈ Z.
) + k2π, k ∈ Z.
c) Đặt t = tanx thì phương trình trở thành 2t2 + 3t + 1 = 0 ⇔ t ∈ {-1 ; ![]() }.
}.
Vậy ![]()
d) Đặt t = tanx thì phương trình trở thành
t - ![]() + 1 = 0 ⇔ t2 + t - 2 = 0 ⇔ t ∈ {1 ; -2}.
+ 1 = 0 ⇔ t2 + t - 2 = 0 ⇔ t ∈ {1 ; -2}.
Vậy ![]()