Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án B
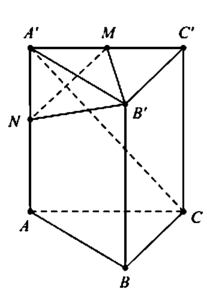Gọi M là trung điểm A’C’. Ta có
B
'
M
⊥
A
C
C
'
A
'
⇒
B
'
M
⊥
A
'
C
.
Suy ra M ∈ m p P . Kẻ M N ⊥ A ' C ( N ∈ A A ' ) ⇒ N ∈ m p P
Thiết diện cắt bởi mặt phẳng (P) và lăng trụ là tan giác B’MN
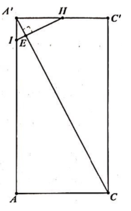
Hai tam giac A’C’C và NA’M đồng dạng ⇒ A ' N = 1 2 A ' M = a 4
Thể tích tứ diện A'B'MN là V 1 = 1 3 A ' N . S ∆ A ' B ' M = a 3 3 96
Thể tích lăng trụ là V = A A ' . S ∆ A B C = a 3 3 2 . Vậy V 1 V 2 = 1 47 .
Chọn đáp án D
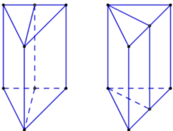
Hình lăng trụ tam giác đều có 4 mặt phẳng đối xứng
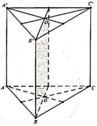
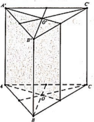
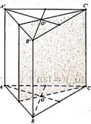
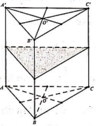
Đáp án B
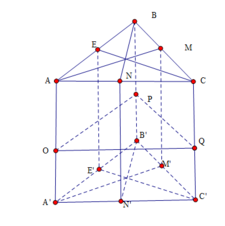
Hình lăng trụ tam giác đều có bốn mặt đối xứng là: ( A , A M M , ) , ( B , B N N , ) , ( C , C E E , ) và(OPQ) (với O,P,Q là trung điểm các cạnh A A , , B B , , C C ,
Hình lăng trụ tam giác đều có mặt phẳng đối xứng (hình vẽ bên dưới).
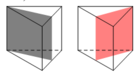
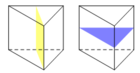
Chọn D.
Chọn đáp án C
Phương pháp
Sử dụng lý thuyết khối đa diện.
Cách giải
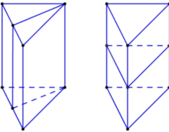
Hình lăng trụ tam giác đều có 4 mặt phẳng đối xứng như hình vẽ bên dưới, trong đó:
+) 3 mặt phẳng tạo bởi 1 cạnh bên và trung điểm của các cạnh đối diện.
+) 1 mặt phẳng tạo bởi trung điểm của 3 cạnh bên
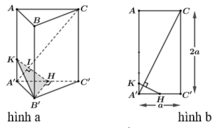
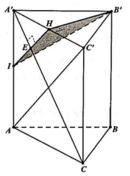
Gọi H là trung điểm của A'C', suy ra 
Trong mặt phẳng (ACC'A') kẻ 
Do đó thiết diện tạo bởi mặt phẳng (P) và khối lăng trụ là tam giác HKB'
Ta có 
và tính được 
Do đó 
Chọn D.
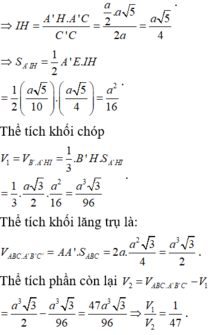
Đáp án B
Số mặt phẳng đối xứng cần tìm là 4.