Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Thành phố A có đúng 12 giờ có ánh sáng mặt trời thì d(t)=12
Khi đó
\(\begin{array}{l}12 = 3\sin \left[ {\frac{\pi }{{182}}\left( {t - 80} \right)} \right] + 12\\ \Leftrightarrow \sin \left[ {\frac{\pi }{{182}}\left( {t - 80} \right)} \right] = 0\\ \Leftrightarrow \sin \left[ {\frac{\pi }{{182}}\left( {t - 80} \right)} \right] = \sin 0\\ \Leftrightarrow \frac{\pi }{{182}}\left( {t - 80} \right) = k\pi \\ \Leftrightarrow t = 80 + 182k;k \in Z\end{array}\)
Mà \(t \in \mathbb{Z}\) và \(0 < t \le 365\) nên
\(\begin{array}{l}0 < 80 + 182k \le 365\\ \Rightarrow 0 \le k \le 1,56\end{array}\)
Suy ra \(k \in \left\{ {0;1} \right\}\)
Khi đó \(t \in \left\{ {80;262} \right\}\)
Vậy Thành phố A có đúng 12 giờ có ánh sáng mặt trời vào ngày thứ 80 và 262 trong năm
b) Thành phố A có đúng 9 giờ có ánh sáng mặt trời thì d(t)=9
Khi đó
\(\begin{array}{l}9 = 3\sin \left[ {\frac{\pi }{{182}}\left( {t - 80} \right)} \right] + 12\\ \Leftrightarrow \sin \left[ {\frac{\pi }{{182}}\left( {t - 80} \right)} \right] = - 1\\ \Leftrightarrow \sin \left[ {\frac{\pi }{{182}}\left( {t - 80} \right)} \right] = \sin \left( { - \frac{\pi }{2}} \right)\\ \Leftrightarrow \frac{\pi }{{182}}(t - 80) = - \frac{\pi }{2} + k2\pi \\ \Leftrightarrow t = - 11 + 364k;k \in Z\end{array}\)
Mà \(t \in \mathbb{Z}\) và \(0 < t \le 365\) nên
\(\begin{array}{l}0 < - 11 + 364k \le 365\\ \Rightarrow 0 < k \le 1,03\end{array}\)
Suy ra \(k= 1\)
Khi đó \(t= - 11 + 364.1 = 353\)
Vậy Thành phố A có đúng 12 giờ có ánh sáng mặt trời vào ngày thứ 353 trong năm
c) Thành phố A có đúng 15 giờ có ánh sáng mặt trời thì d(t)=15
Khi đó
\(\begin{array}{l}15 = 3\sin \left[ {\frac{\pi }{{182}}\left( {t - 80} \right)} \right] + 12\\ \Leftrightarrow \sin \left[ {\frac{\pi }{{182}}\left( {t - 80} \right)} \right] = 1\\ \Leftrightarrow \sin \left[ {\frac{\pi }{{182}}\left( {t - 80} \right)} \right] = \sin \left( {\frac{\pi }{2}} \right)\\ \Leftrightarrow \frac{\pi }{{182}}(t - 80) = \frac{\pi }{2} + k2\pi \\ \Leftrightarrow t = 171 + 364k;k \in Z\end{array}\)
Mà \(t \in \mathbb{Z}\) và \(0 < t \le 365\) nên
\(\begin{array}{l}0 < 171 + 364k \le 365\\ \Rightarrow 0 \le k \le 0,53\end{array}\)
Suy ra \(k=0\)
Khi đó \(t= 171 + 364.0 = 171\)
Vậy Thành phố A có đúng 12 giờ có ánh sáng mặt trời vào ngày thứ 171 trong năm

\(\begin{array}{l} - 1 \le sin\frac{\pi }{{12}}(t - 9)\; \le 1\\ \Leftrightarrow - 3 \le 3sin\frac{\pi }{{12}}(t - 9)\; \le 3\\ \Leftrightarrow - 26 \le 29 + 3sin\frac{\pi }{{12}}(t - 9)\; \le 32\\ \Leftrightarrow - 26 \le h(t) \le 32\end{array}\)
Vâỵ nhiệt độ thấp nhất trong ngày là 26°C khi:
\(\begin{array}{l}29 + 3sin\frac{\pi }{{12}}(t - 9) = 26\\ \Leftrightarrow sin\frac{\pi }{{12}}(t - 9) = - 1\\ \Leftrightarrow \frac{\pi }{{12}}(t - 9) = - \frac{\pi }{2} + k2\pi \\ \Leftrightarrow t = 3 + 24k,k \in \mathbb{Z}.\end{array}\)
Do t là thời gian trong ngày tính bằng giờ nên \(0 \le t \le 24\). Suy ra: \(k = 0 \Rightarrow t = 3\).
Vì vậy vào thời điểm 3 giờ trong ngày thì nhiều độ thấp nhất của thành phố là 26°C.
Đáp án: C

Ta có: (x3 +
)8=Ck8 x3(8 – k) ()k =Ck8 x24 – 4k
Trong tổng này, số hạng Ck8 x24 – 4k không chứa x khi và chỉ khi

a) Giả sử dân số của thành phố đó từ năm 2022 là dãy số \(\left( {{u_n}} \right)\) với \({u_1} = 2,1\).
Ta có:
\(\begin{array}{l}{u_1} = 2,1\\{u_2} = {u_1} + {u_1}.\frac{{0,75}}{{100}} = {u_1}.\left( {1 + \frac{{0,75}}{{100}}} \right)\\{u_3} = {u_2} + {u_2}.\frac{{0,75}}{{100}} = {u_2}\left( {1 + \frac{{0,75}}{{100}}} \right)\\{u_4} = {u_3} + {u_3}.\frac{{0,75}}{{100}} = {u_3}\left( {1 + \frac{{0,75}}{{100}}} \right)\\ \vdots \\{u_n} = {u_{n - 1}} + {u_{n - 1}}.\frac{{0,75}}{{100}} = {u_{n - 1}}\left( {1 + \frac{{0,75}}{{100}}} \right)\end{array}\)
Vậy dân số của thành phố đó từ năm 2022 tạo thành cấp số nhân với số hạng đầu \({u_1} = 2,1\) và công bội \(q = 1 + \frac{{0,75}}{{100}}\).
Dân số của thành phố đó vào năm 2032 là: \({u_{11}} = {u_1}.{q^{10}} = 2,1.{\left( {1 + \frac{{0,75}}{{100}}} \right)^{10}} \approx 2,26\) (triệu người).
b) Giả sử sau \(n - 1\) năm thì dân số thành phố đó tăng gấp đôi. Khi đó ta có:
\({u_n} = 2{u_1} \Leftrightarrow {u_1}.{q^{n - 1}} = 2{u_1} \Leftrightarrow {q^{n - 1}} = 2 \Leftrightarrow {\left( {1 + \frac{{0,75}}{{100}}} \right)^{n - 1}} = 2 \Leftrightarrow n \approx 93,77 \Rightarrow n = 94\)
Vậy sau 93 năm thì dân số thành phố đó tăng gấp đôi.
Vậy ước tính vào năm 2115 dân số của thành phố đó sẽ tăng gấp đôi so với năm 2022.

Đáp án C.
Các cách đi: ![]() :
: ![]() cách.
cách.
![]() :
: ![]() cách.
cách.
Vậy tất cả có 159 cách đi từ A đến D.
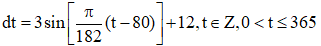
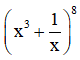


Thành phố A có đúng 12 giờ có ánh sáng mặt trời vào ngày nào trong năm ?
Ta giải phương trình d(t)=12d(t)=12 với t∈Zt∈Z và 0<t≤3650<t≤365
Ta có d(t)=12d(t)=12
⇔3sin(π182(t−80))+12=12⇔3sin(π182(t−80))+12=12
⇔sin[π182(t−80)]=0⇔sin[π182(t−80)]=0
⇔π182(t−80)=kπ⇔π182(t−80)=kπ
⇔t−80=182k⇔t−80=182k
⇔t=182k+80(k∈Z)⇔t=182k+80(k∈Z)
Ta lại có
0<182k+80≤3650<182k+80≤365
⇔−80182<k≤285182⇔−80182<k≤285182
⇔[k=0k=1⇔[k=0k=1
Vậy thành phố AA có đúng 1212 giờ ánh sáng mặt trời vào ngày thứ 8080 (ứng với k=0k=0) và ngày thứ 262262 (ứng với k=1k=1) trong năm.
Vào ngày nào trong năm thì thành phố A có ít giờ có ánh sáng mặt trời nhất ?
Do sin(π182(t−80))≥−1sin(π182(t−80))≥−1 ⇒d(t)≤3.(−1)+12=9⇒d(t)≤3.(−1)+12=9 với mọi xx
Vậy thành phố AA có ít giờ ánh sáng mặt trời nhất khi và chỉ khi :
sin[π182(t−80)]=−1sin[π182(t−80)]=−1 với với t∈Z và 0<t≤365t∈Z và 0<t≤365
Phương trình đó cho ta
π182(t−80)=−π2+k2ππ182(t−80)=−π2+k2π
⇔t−80=182(−12+2k)⇔t−80=182(−12+2k)
⇔t=364k−11(k∈Z)⇔t=364k−11(k∈Z)
Mặt khác,0<364k−11≤3650<364k−11≤365 ⇔11364<k≤376364⇔k=1⇔11364<k≤376364⇔k=1 (do kk nguyên)
Vậy thành phố AA có ít giờ ánh sáng mặt trời nhất (99 giờ) khi t=353t=353, tức là vào ngày thứ 353353 trong năm.