
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

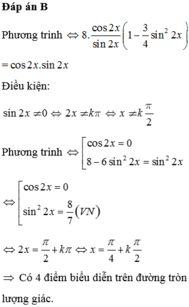


Chọn C
Ta có: ![]() nên (1) và (2) có nghiệm.
nên (1) và (2) có nghiệm.
Cách 1:
Xét: ![]()
![]() nên (3) vô nghiệm.
nên (3) vô nghiệm.
Cách 2:
Điều kiện có nghiệm của phương trình: sin x + cos x = 2 là: 
(vô lý) nên (3) vô nghiệm.
Cách 3:
Vì 

nên (3) vô nghiệm.

Tính \(I=\int_0^{\dfrac{\pi}{2}}\dfrac{cos^{2017}x}{sin^{2017}x+cos^{2017}}dx\left(1\right)\)
Đặt \(t=cosx\Rightarrow sinx=\sqrt{1-cos^2x}\)
\(\Rightarrow dt=-sinx.dx\)
\(\Rightarrow I=\int_0^1\dfrac{t^{2017}.}{\sqrt{1-t^2}.\left(\left(\sqrt{1-t^2}\right)^{2017}+t^{2017}\right)}dt\)
Đặt: \(t=siny\Rightarrow\sqrt{1-t^2}=cosy\)
\(\Rightarrow dt=cosy.dy\)
\(\Rightarrow I=\int_0^{\dfrac{\pi}{2}}\dfrac{sin^{2017}y.cosy}{cosy\left(cos^{2017}y+sin^{2017}y\right)}dy=\int_0^{\dfrac{\pi}{2}}\dfrac{sin^{2017}y}{\left(cos^{2017}y+sin^{2017}y\right)}\)
\(\Rightarrow I=\int_0^{\dfrac{\pi}{2}}\dfrac{sin^{2017}x}{\left(cos^{2017}x+sin^{2017}x\right)}\left(2\right)\)
Cộng (1) và (2) ta được
\(2I=\int_0^{\dfrac{\pi}{2}}\dfrac{sin^{2017}x+cos^{2017}x}{sin^{2017}x+cos^{2017}x}dx=\int_0^{\dfrac{\pi}{2}}1dx\)
\(=x|^{\dfrac{\pi}{2}}_0=\dfrac{\pi}{2}\)
\(\Rightarrow I=\dfrac{\pi}{4}\)
Thế lại bài toán ta được
\(\dfrac{\pi}{4}+t^2-6t+9-\dfrac{\pi}{4}=0\)
\(\Leftrightarrow t^2-6t+9=0\)
\(\Leftrightarrow t=3\)
Chọn đáp án C
mỗi trắc nghiệm thoy mà lm dài ntn s @@
chắc lên đó khó lắm ag

Đường tròn (S) tâm \(I\left(-1;-3\right)\) bán kính \(R=3\)
Thế tọa độ A vào pt (S) thỏa mãn nên A nằm trên đường tròn
Ta cần tìm B, C sao cho chi vi ABC lớn nhất
Đặt \(\left(AB;AC;BC\right)=\left(c;b;a\right)\Rightarrow\dfrac{a}{sinA}=\dfrac{b}{sinB}=\dfrac{c}{sinC}=2R\)
\(\Rightarrow a+b+c=2R\left(sinA+sinB+sinC\right)\)
Mặt khác ta có BĐT quen thuộc \(sinA+sinB+sinC\le\dfrac{3\sqrt{3}}{2}\)
Dấu "=" xảy ra khi tam giác ABC đều
\(\Rightarrow a=b=c=2R.sin60^0=3\sqrt{3}\)
Khi đó I đồng thời là trọng tâm kiêm trực tâm \(\Rightarrow\left\{{}\begin{matrix}BC\perp AI\\d\left(A;BC\right)=\dfrac{a\sqrt{3}}{2}=\dfrac{9}{2}\end{matrix}\right.\)
\(\Rightarrow\) Phương trình BC có dạng \(y=-\dfrac{3}{2}\)
Hay (Cm) có 1 tiếp tuyến là \(y=-\dfrac{3}{2}\) (hệ số góc bằng 0 nên tiếp tuyến này đi qua 2 cực tiểu)
\(\Rightarrow m=-1\)

1.
PT $\Leftrightarrow 2^{x^2-5x+6}+2^{1-x^2}-2^{7-5x}-1=0$
$\Leftrightarrow (2^{x^2-5x+6}-2^{7-5x})-(1-2^{1-x^2})=0$
$\Leftrightarrow 2^{7-5x}(2^{x^2-1}-1)-(2^{x^2-1}-1)2^{1-x^2}=0$
$\Leftrightarrow (2^{x^2-1}-1)(2^{7-5x}-2^{1-x^2})=0$
$\Rightarrow 2^{x^2-1}-1=0$ hoặc $2^{7-5x}-2^{1-x^2}=0$
Nếu $2^{x^2-1}=1\Leftrightarrow x^2-1=0$
$\Leftrightarrow x^2=1\Leftrightarrow x=\pm 1$
$2^{7-5x}-2^{1-x^2}=0$
$\Leftrightarrow 7-5x=1-x^2\Leftrightarrow x^2-5x+6=0$
$\Leftrightarrow (x-2)(x-3)=0\Leftrightarrow x=2; x=3$
2. Đặt $\sin ^2x=a$ thì $\cos ^2x=1-a$. PT trở thành:
$16^a+16^{1-a}=10$
$\Leftrightarrow 16^a+\frac{16}{16^a}=10$
$\Leftrightarrow (16^a)^2-10.16^a+16=0$
Đặt $16^a=x$ thì:
$x^2-10x+16=0$
$\Leftrightarrow (x-2)(x-8)=0$
$\Leftrightarrow x=2$ hoặc $x=8$
$\Leftrightarrow 16^a=2$ hoặc $16^a=8$
$\Leftrightarrow 2^{4a}=2$ hoặc $2^{4a}=2^3$
$\Leftrightarroww 4a=1$ hoặc $4a=3$
$\Leftrightarrow a=\frac{1}{4}$ hoặc $a=\frac{3}{4}$
Nếu $a=\frac{1}{4}\Leftrightarrow \sin ^2x=\frac{1}{4}$
$\Leftrightarrow \sin x=\pm \frac{1}{2}$
Nếu $a=\sin ^2x=\frac{3}{4}\Rightarrow \sin x=\pm \frac{\sqrt{3}}{2}$
Đến đây thì đơn giản rồi.

a.
\(y'=-\dfrac{3}{2}x^3+\dfrac{6}{5}x^2-x+5\)
b.
\(y'=\dfrac{\left(x^2+4x+5\right)'}{2\sqrt{x^2+4x+5}}=\dfrac{2x+4}{2\sqrt{x^2+4x+5}}=\dfrac{x+2}{\sqrt{x^2+4x+5}}\)
c.
\(y=\left(3x-2\right)^{\dfrac{1}{3}}\Rightarrow y'=\dfrac{1}{3}\left(3x-2\right)^{-\dfrac{2}{3}}=\dfrac{1}{3\sqrt[3]{\left(3x-2\right)^2}}\)
d.
\(y'=2\sqrt{x+2}+\dfrac{2x-1}{2\sqrt{x+2}}=\dfrac{6x+7}{2\sqrt{x+2}}\)
e.
\(y'=3sin^2\left(\dfrac{\pi}{3}-5x\right).\left[sin\left(\dfrac{\pi}{3}-5x\right)\right]'=-15sin^2\left(\dfrac{\pi}{3}-5x\right).cos\left(\dfrac{\pi}{3}-5x\right)\)
g.
\(y'=4cot^3\left(\dfrac{\pi}{6}-3x\right)\left[cot\left(\dfrac{\pi}{3}-3x\right)\right]'=12cot^3\left(\dfrac{\pi}{6}-3x\right).\dfrac{1}{sin^2\left(\dfrac{\pi}{3}-3x\right)}\)