
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


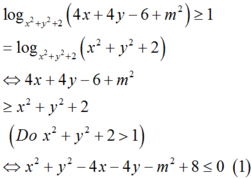
Ta có
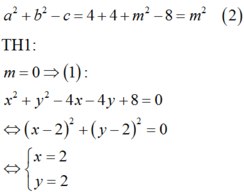
Cặp số x ; y = 2 ; 2 không thỏa mãn điều kiện .
![]()
Tập hợp các cặp số (x;y) thỏa mãn (1) là hình tròn C1(kể cả biên) tâm I1(2;2) bán kính R 1 = m .
Tập hợp các cặp số (x;y) thỏa mãn (2) là đường tròn C2 tâm I 2 - 1 ; 2 bán kính R 2 = 1 + 4 - 1 = 2 .
Để tồn tại duy nhất cặp số (x;y) thỏa mãn 2 điều kiện (1) và (2) Xảy ra 2 trường hợp sau:
TH1: C1; C2tiếp xúc ngoài
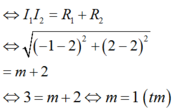
TH2: C1; C2 tiếp xúc trong và
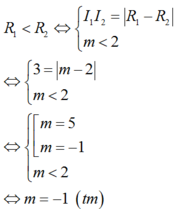
Vậy S = - 1 ; 1 .
Chọn D.

Chọn đáp án B
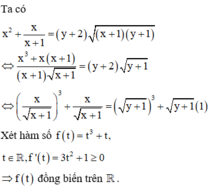
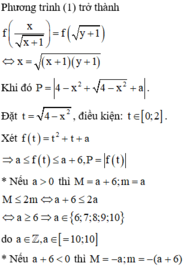
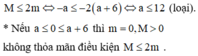
Vậy có 5 giá trị nguyên của m thỏa mãn điều kiện.

Đáp án D
Ta có: 4 x − m .2 x + 1 + 2 m = 0 ⇔ 2 x 2 − 2 m .2 x + 2 m = 0
Giả thiết ⇔ Δ ' = m 2 − 2 m > 0 S = 2 m > 0 P = 2 m > 0 ⇔ m > 2
Khi đó: 2 x 1 + 2 x 2 = 2 m 2 x 1 .2 x 2 = 2 m ⇔ 2 x 1 + x 2 = 2 m ⇔ m = 4
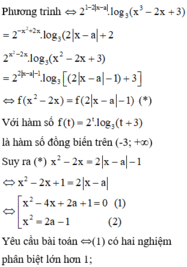
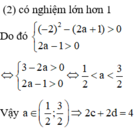
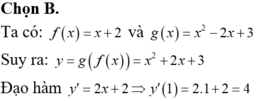
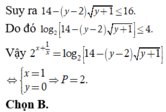


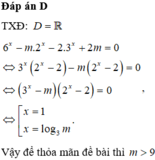
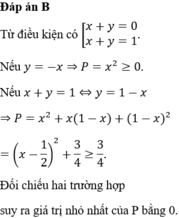

\(\left(x^2-2x\right)\left|3x-7\right|=0\)
\(\Rightarrow x^2-2x=0\) hoặc \(\left|3x-7\right|=0\)
+ \(x^2-2x=0 \)
\(x\left(x-2\right)=0\)
\(\int_{x-2=0\Rightarrow x=2}^{x=0}\)
+, |3x-7|=0
=> 3x-7=0
3x =7
x = 7:3
x = 7/3
Vậy \(x\in\left\{0,2,\frac{7}{3}\right\}\)
BAI nay lop may vay