Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(C=\dfrac{-5}{7}+\dfrac{-2}{7}+\dfrac{3}{4}+\dfrac{1}{4}+\dfrac{-1}{5}=-1+1-\dfrac{1}{5}=\dfrac{-1}{5}\)

\(\dfrac{-1}{12},\dfrac{-3}{4},\dfrac{2}{9},\dfrac{7}{6}\)

`1/5 . 4/7 + 3/7 . 1/5 -1/5`
`=1/5 . 4/7 + 3/7 . 1/5 -1/5 . 1`
`=1/5 . ( 4/7+3/7-1)`
`=1/5 . ( 7/7-1)`
`= 1/5 . 0`
`=0`
\(\dfrac{1}{5}\times\dfrac{4}{7}+\dfrac{3}{7}\times\dfrac{1}{5}-\dfrac{1}{5}=\dfrac{1}{5}\times\left(\dfrac{4}{7}+\dfrac{3}{7}-1\right)=\dfrac{1}{5}\times0=0\)

\(-\dfrac{5}{7}\times\dfrac{2}{13}+\dfrac{-5}{7}\times\dfrac{3}{13}-\dfrac{5}{7}\times\dfrac{8}{13}\)
\(=-\dfrac{5}{7}\left(\dfrac{2}{13}+\dfrac{3}{13}+\dfrac{8}{13}\right)\)
\(=-\dfrac{5}{7}\times\dfrac{13}{13}\)
\(=-\dfrac{5}{7}\times1=-\dfrac{5}{7}\)

\(-\dfrac{3}{7}\times\dfrac{15}{13}-\dfrac{3}{7}\times\dfrac{11}{13}-\dfrac{3}{7}\)
\(=-\dfrac{3}{7}\left(\dfrac{15}{13}+\dfrac{11}{13}+1\right)\)
\(=-\dfrac{3}{7}\left(\dfrac{15}{13}+\dfrac{11}{13}+\dfrac{13}{13}\right)\)
\(=-\dfrac{3}{7}\times\dfrac{39}{13}=-\dfrac{3}{7}\times3=-\dfrac{9}{7}\)

\(\dfrac{-1}{9}.\dfrac{-3}{5}+\dfrac{5}{-6}.\dfrac{-3}{5}-\dfrac{7}{2}.\dfrac{3}{5}\)
\(=\dfrac{3}{5}.\left(\dfrac{1}{9}+\dfrac{5}{6}-\dfrac{7}{2}\right)\)
\(=\dfrac{3}{5}.\left(\dfrac{2}{18}+\dfrac{15}{18}-\dfrac{63}{18}\right)\)
\(=\dfrac{3}{5}.\left(-\dfrac{23}{9}\right)\)
\(=-\dfrac{69}{45}\)

`6/7 . 8/13 +6/7 . 9/13+3/13 . 6/7`
`=6/7 . (8/13+9/13+3/13)`
`=6/7 . 20/13`
`=120/91`
\(\dfrac{6}{7}.\dfrac{8}{13}+\dfrac{6}{7}.\dfrac{9}{13}+\dfrac{3}{13}.\dfrac{6}{7}\)
\(=\dfrac{6}{7}.\left(\dfrac{8}{13}+\dfrac{9}{13}+\dfrac{3}{13}\right)\)
\(=\dfrac{6}{7}.\left(\dfrac{8+9+3}{13}\right)\)
\(=\dfrac{6}{7}.\dfrac{20}{13}\)
\(=\dfrac{6.20}{7.13}\)
\(=\dfrac{120}{91}\)

a) \(x=\dfrac{-2}{7}+\dfrac{9}{7}=1\)
b) \(\dfrac{x}{3}=\dfrac{2}{5}+\dfrac{-4}{3}\)
\(\dfrac{x}{3}=\dfrac{-14}{15}\)
\(\Rightarrow x=\dfrac{3.-14}{15}=\dfrac{-14}{5}\)
\(x=\dfrac{-2}{7}+\dfrac{9}{7}\)
\(x=1\)
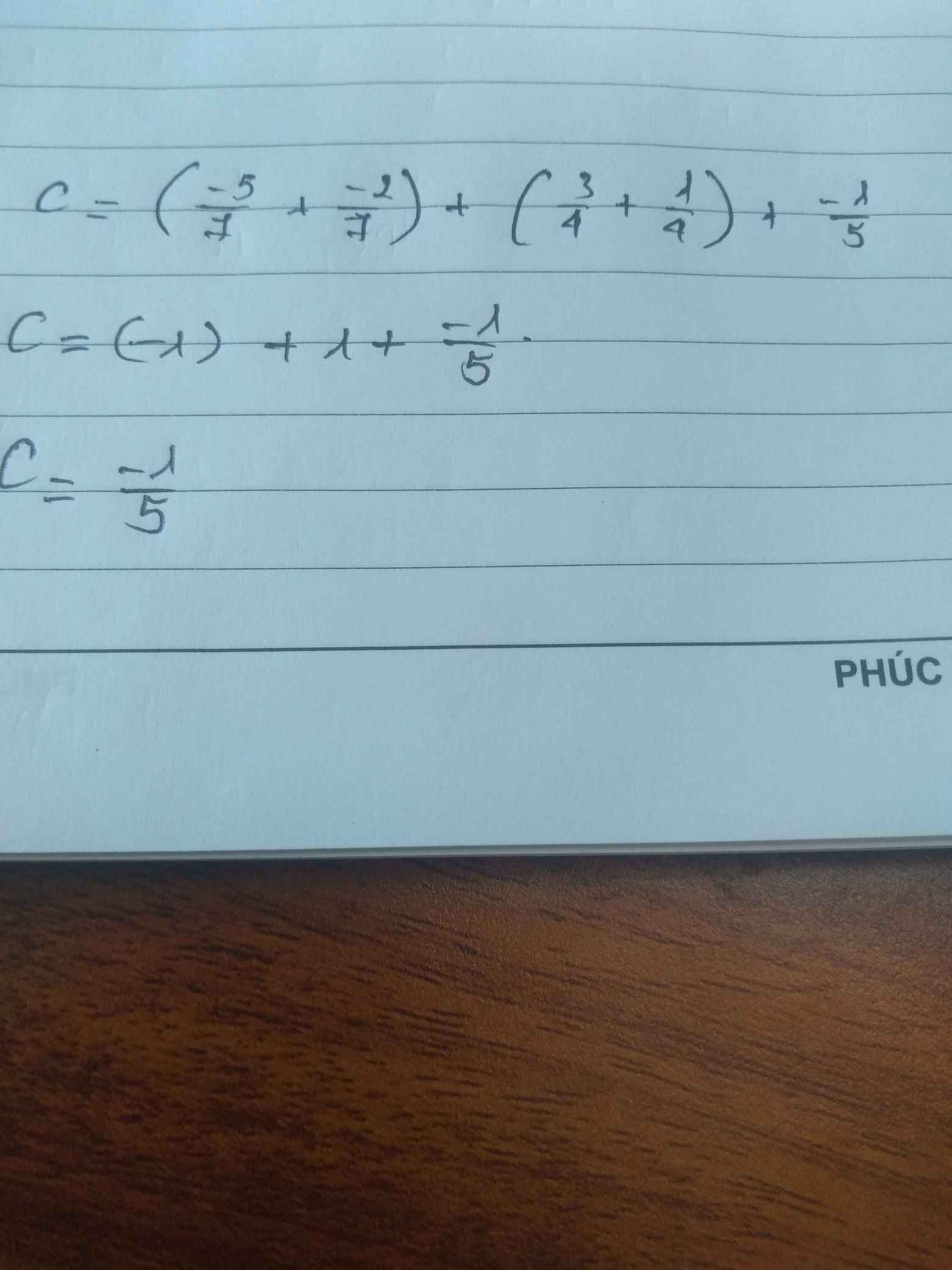
Lời giải:
$S=\frac{1}{7^2}+\frac{2}{7^3}+\frac{3}{7^4}+...+\frac{69}{7^{70}}$
$7S=\frac{1}{7}+\frac{2}{7^2}+\frac{3}{7^3}+...+\frac{69}{7^{69}}$
$6S=7S-S=\frac{1}{7}+\frac{1}{7^2}+\frac{1}{7^3}+....+\frac{1}{7^{69}}-\frac{69}{7^{70}}$
$42S=1+\frac{1}{7}+\frac{1}{7^2}+...+\frac{1}{7^{68}}-\frac{69}{7^{69}}$
$\Rightarrow 42S-6S=(1+\frac{1}{7}+\frac{1}{7^2}+...+\frac{1}{7^{68}}-\frac{69}{7^{69}})-(\frac{1}{7}+\frac{1}{7^2}+\frac{1}{7^3}+....+\frac{1}{7^{69}}-\frac{69}{7^{70}})$
$\Rightarrow 36S=1-\frac{69}{7^{69}}-\frac{1}{7^{69}}+\frac{69}{7^{70}}$
Hay $36S=1-\frac{69.7-7-69}{7^{70}}=1-\frac{407}{7^{70}}$
$\Rightarrow S=\frac{1}{36}(1-\frac{407}{7^{70}})$