Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(-2< -1,75< 0< \sqrt{5}< \pi< \dfrac{22}{7}< 5\dfrac{3}{6}.\)

Ta có:
\(-\frac{2}{3} = -0,\left( 6 \right);\,\,\,\,\,4,1;\,\,\, - \sqrt 2 = - 1,414...;\,\,\,\,3,2;\\\pi = 3,141...;\,\,\,\, - \frac{3}{4} = - 0,75;\,\,\,\,\frac{7}{3} = 2,\left( 3 \right)\).
Do \( - 1,414... < - 0,75 < -0,\left( 6 \right) < 2,\left( 3 \right) < 3,141... < 3,2 < 4,1\)
Nên \( - \sqrt 2 < - \frac{3}{4} < -\frac{2}{3} < \frac{7}{3} < \pi < 3,2 < 4,1.\)

a: \(-3< -2.15< -\sqrt{3}< 0< \dfrac{13}{7}< \sqrt{8}< \dfrac{33}{12}\)
b: \(0< \sqrt{3}< \dfrac{13}{7}< 2.15< \dfrac{33}{12}< \sqrt{8}< 3\)

Bài 2 :
Giả sử \(a=\sqrt{3}\)là số hữu tỉ
Khi đó ta có \(a=\sqrt{3}=\frac{m}{n}\)với m, n tối giản ( n khác 0 )
Từ \(\sqrt{3}=\frac{m}{n}\Rightarrow m=\sqrt{3}n\)
Bình phương 2 vế ta được đẳng thức: \(m^2=3n^2\)(*)
\(\Rightarrow m^2⋮3\)mà m tối giản \(\Rightarrow m⋮3\)
=> m có dạng \(3k\)
Thay m vào (*) ta có : \(9k^2=3n^2\)
\(\Leftrightarrow3k^2=n^2\)
\(\Leftrightarrow n=\sqrt{3}k\)
Vì k là số nguyên => n không là số nguyên
=> điều giả sử là sai
=> \(\sqrt{3}\)là số vô tỉ

a)-3<-2<-\(\sqrt[]{3}\)<0<\(\dfrac{13}{7}\)<\(\dfrac{33}{12}\)<\(\sqrt{8}\)<15
b)|0|<|-\(\sqrt{3}\)|\(\dfrac{13}{7}\)|<|-2|<|\(\dfrac{33}{12}\)|<\(\sqrt{8}\)<|-3|<15

\(\left| { - 3,2} \right| = 3,2;\,\,\,\,\,\left| {2,13} \right| = 2,13;\,\,\,\left| {\, - \sqrt 2 } \right| = \sqrt 2 = 1,41..;\,\,\,\,\left| { - \frac{3}{7}} \right| = \frac{3}{7} = 0,42...\)
Do \(0,42 < 1,41... < 2,13 < 3,2\) nên:
\(\left| { - \frac{3}{7}} \right| < \left| { - \sqrt 2 } \right| < \left| {2,13} \right| < \left| { - 3,2} \right|\).

Giải :
-3 = -3
2 = 2
2,13 = 2,13
-√2 = -1,414
\(\frac{3}{7}\)= 0,428
⇒ -3 < -√2 < \(\frac{3}{7}\) < 2 < 2,13
CHÚC BẠN HỌC TỐT ^_^
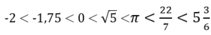
Nguyễn Ngọc Quý sư cô là số pi=3,14