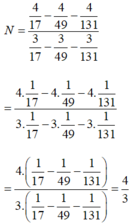Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
\(A=1+3+(3^2+3^3+3^4+3^5)+(3^6+3^7+3^8+3^9)+...+(3^{46}+3^{47}+3^{48}+3^{49})\)
\(=4+3^2(1+3+3^2+3^3)+3^6(1+3+3^2+3^3)+....+3^{46}(1+3+3^2+3^3)\)
\(=4+3^2.40+3^6.40+....+3^{46}.40\)
\(=10(4.3^2+4.3^6+..+4.3^{46})+4\)
Vậy $A$ có tận cùng là $4$


a) cách 1 :
\(-5\left(32-36\right)+\left(31-39\right)=-5.\left(-4\right)+\left(-8\right)=12\)
cách 2 ;
\(-5\left(32-36\right)+\left(31-39\right)=-5.32-\left(-5.36\right)+\left(-8\right)=-160-\left(-180\right)+8=12\)
b) cách 1
\(-2\left(15-27\right)-4\left(12-8\right)=-2.\left(-12\right)-4.4=24-16=8\)
cách 2:
\(-2\left(15-27\right)-4\left(12-8\right)=-2.15-\left(-2.27\right)-4.12-4.\left(8\right)=-30-\left(-54\right)-48-\left(-32\right)=8\)

\(\Leftrightarrow-B=1+3+3^2+...+3^{49}\\ \Leftrightarrow-3B=3+3^2+3^3+...+3^{50}\\ \Leftrightarrow-3B-B=3+3^2+...+3^{50}-1-3-...-3^{49}\\ \Leftrightarrow-4B=3^{50}-1\\ \Leftrightarrow B=\dfrac{1-3^{50}}{4}\)

Đáp án A
N = 4 17 - 4 49 - 4 131 3 17 - 3 49 - 3 131 = 4 . 1 17 - 4 . 1 49 - 4 . 1 131 3 . 1 17 - 3 . 1 49 - 3 . 1 131 = 4 1 17 - 1 49 - 1 131 3 1 17 - 1 49 - 1 131 = 4 3

Đáp án A
N = 4 17 - 4 49 - 4 131 3 17 - 3 49 - 3 131 = 4 . 1 17 - 4 . 1 49 - 4 . 1 131 3 . 1 17 - 3 . 1 49 - 3 . 1 131 = 4 1 17 - 1 49 - 1 131 3 1 17 - 1 49 - 1 131 = 4 3