
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Có thể hiểu nôm na là khi tính vecto pháp tuyến, chỉ phương hoặc cần tỉ lệ để tính song song thì có thể "rút gọn", còn khi tính độ dài, tính góc thì không được (tính toán liên quan độ dài thì tuyệt đối ko được "rút gọn" vecto, còn tính toán góc thì chỉ rút gọn khi thực sự hiểu).

\(=sin^2x\cdot sin^2x\cdot\dfrac{cos^2x}{sin^2x}+cos^4x\cdot\dfrac{sin^2x}{cos^2x}+sin^4x\cdot sin^2x\cdot cos^2x\)
\(=sin^2x\cdot cos^2x+sin^2x\cdot cos^2x+sin^4x\cdot sin^2x\cdot cos^2x\)
\(=sin^2x\cdot cos^2x\cdot\left(sin^4x+2\right)\)

Chọn C.
Ta có: cot2a - cos2a
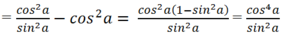
Tương tự ta có; tan2a - sin2a =
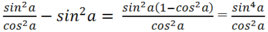
Do đó
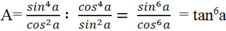

\(B=cos\left(\pi+\dfrac{\pi}{2}-a\right)-sin\left(8\pi-a\right)+tan\left(3\pi+\dfrac{\pi}{2}-a\right)+cot\left(3\pi-a\right)\)
\(=-cos\left(\dfrac{\pi}{2}-a\right)-sin\left(-a\right)+tan\left(\dfrac{\pi}{2}-a\right)+cot\left(-a\right)\)
\(=-sina+sina+cota-cota=0\)
\(C=sin\left(a+\dfrac{\pi}{2}+42\pi\right)-cos\left(2022\pi-a\right)+sin^2\left(33\pi+a\right)+sin^2\left(a-\dfrac{\pi}{2}-2\pi\right)\)
\(=sin\left(a+\dfrac{\pi}{2}\right)-cosa+sin^2a+sin^2\left(\dfrac{\pi}{2}-a\right)\)
\(=cosa-cosa+sin^2a+cos^2a=1\)
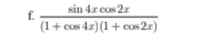
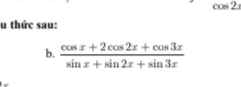
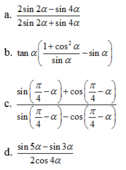

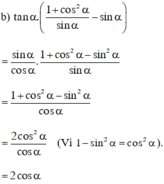
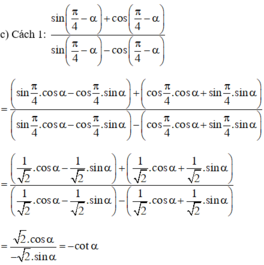
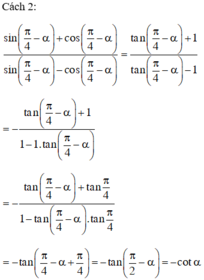
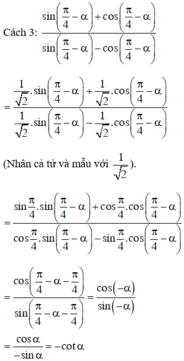
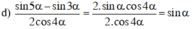
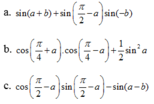
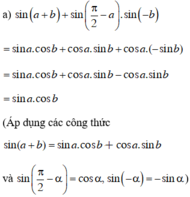
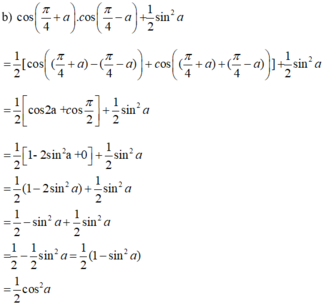
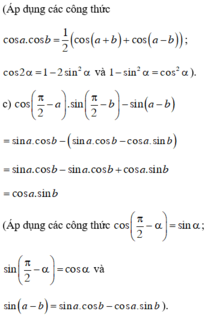
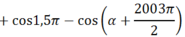
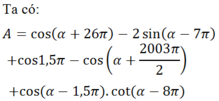
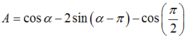
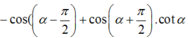
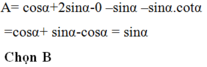
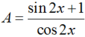 ta được
ta được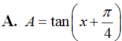
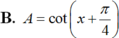
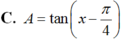
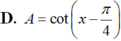
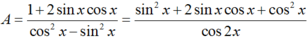
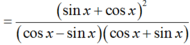
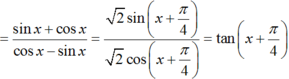
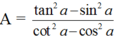 bằng :
bằng :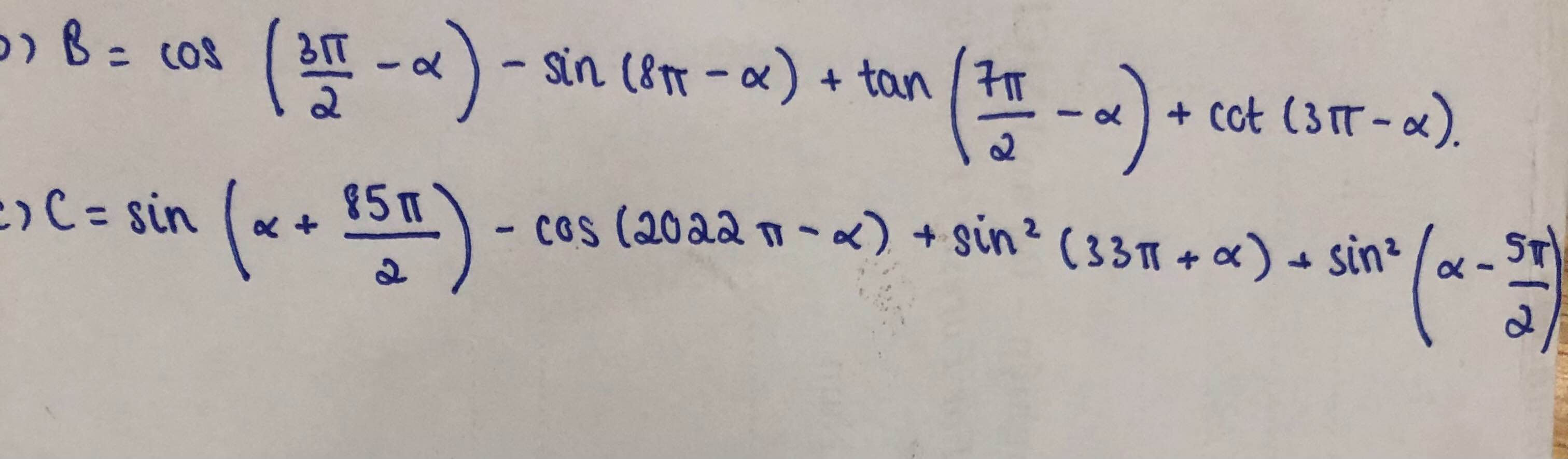
\(=\dfrac{2sin2x.cos^22x}{\left(1+2cos^22x-1\right)\left(1+2cos^2x-1\right)}=\dfrac{4sinx.cosx.cos^22x}{4cos^22x.cos^2x}\)
\(=\dfrac{sinx}{cosx}=tanx\)
Em cảm ơn ạ (◍•ᴗ•◍)❤