K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NH
1
4 tháng 7 2023
1: \(=\dfrac{x-1}{x^2+x+1}+\dfrac{x+1}{x-1}\)
\(=\dfrac{x^2-2x+1+x^3+x^2+x^2+x+x+1}{\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\dfrac{x^3+3x^2+2}{\left(x-1\right)\left(x^2+x+1\right)}\)
2: \(=\dfrac{\left(x^2-y^2\right)^2}{\left(x-y\right)\left(x^2+xy+y^2\right)}=\dfrac{\left(x-y\right)\left(x+y\right)^2}{x^2+xy+y^2}\)
25 tháng 9 2021
1)
a) \(=3x^2\left(x^2-1\right)-\left(x^3-1\right)+x^8-3x^4+3x^2-1\)
\(=3x^4-3x^2-x^3+1+x^8-3x^4+3x^2-1=x^8-x^3\)
2)
\(=\left(x^2+5x-6\right)\left(x^2+5x+6\right)-6\left(x^2+5x\right)+45\)
\(=\left(x^2+5x\right)^2-6\left(x^2+5x\right)-36+45\)
\(=\left(x^2+5x\right)^2-6\left(x^2+5x\right)+9=\left(x^2+5x-3\right)^2\)
PT
1
PT
1
13 tháng 11 2021
2: \(=\dfrac{\left(x-y\right)\left(x+y\right)\left(x^2+y^2\right)}{-\left(x-y\right)\left(x^2+xy+y^2\right)}=\dfrac{-\left(x+y\right)\left(x^2+y^2\right)}{x^2+xy+y^2}\)
CM
30 tháng 9 2019
A = ( x 2 + 2 – 2 x ) ( x 2 + 2 + 2 x ) – x 4 = x 2 . x 2 + 2 . x 2 + 2 x . x 2 + 2 . x 2 + 2 . 2 + 2 . 2 x – 2 x . x 2 – 2 . 2 x – 2 x . 2 x – x 4 = x 4 + 2 x 2 + 2 x 3 + 2 x 2 + 4 + 4 x – 2 x 3 – 4 x – 4 x 2 – x 4
= 4
Vậy A = 4
Đáp án cần chọn là: A
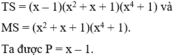
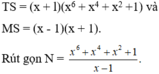
Theo cách mình nghĩ thì :
= (x6 - 3x4 + 3x2 - 1) x2 (x2 +1) (1 - 1)
= x2 (x2 + 1)
=> x2 = 0 => x = 0
=> x2 + 1 => x2 = -1 => x thuộc rỗng (loại)
Vậy : x =0
Ay ya, nhầm rồi, chỉ tới cái khúc = x2 (x2 + 1 ) thôi nhé