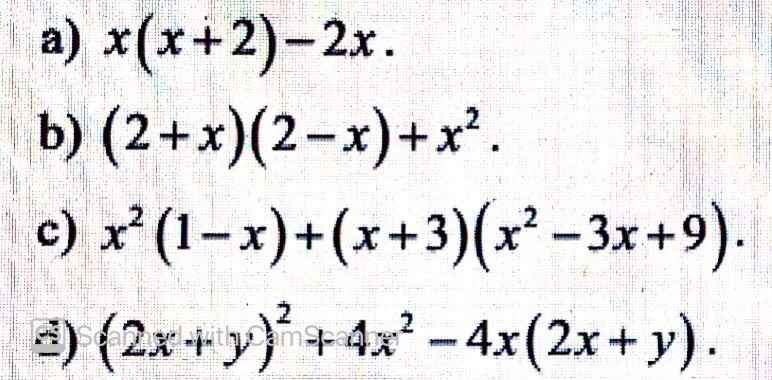H
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
D
1
13 tháng 11 2023
\(\left(a-b+c\right)^2-\left(b-c\right)^2+2ab-2ac\)
\(=a^2-2a\left(b-c\right)+\left(b-c\right)^2-\left(b-c\right)^2+2a\left(b-c\right)\)
\(=a^2-2a\left(b-c\right)+2a\left(b-c\right)\)
\(=a^2\)
21 tháng 12 2019
a) Giá trị của phân thức được xác định
\(\Leftrightarrow x^2-1\ne0\)
\(\Leftrightarrow x\ne\pm1\)
Vậy để giá trị của phân thức đã cho xác định \(\Leftrightarrow x\ne\pm1\)
b)Ta có:
\(\frac{3x+3}{x^2-1}=\frac{3\left(x+1\right)}{\left(x+1\right)\left(x-1\right)}=\frac{3}{x-1}\)
c) Để phân thức nhận giá trị nguyên dương
\(\Leftrightarrow\frac{3}{x-1}\)có giá trị nguyên dương
\(\Leftrightarrow x-1\)\(\inƯ\left(3\right)=\left\{1;3\right\}\)
| x-1 | 1 | 3 |
| x | 2 ( Nhận ) | 4 ( Nhận ) |
Vậy với \(x\in\left\{2;4\right\}\)thì giá trị của phân thức có giá trị nguyên dương.
HH
2
TT
2 tháng 8 2019
P = 9x2 + 24x + 16 -10x - x2 +16
P = 8x2 +14x +32
P = 2(4x2 + 7x +16)
6 tháng 8 2020
P = ( 3x + 4 )2 - 10x - ( x - 4 )( x + 4 )
P = 9x2 + 24x + 16 - 10x - ( x2 - 16 )
P = 9x2 + 24x + 16 - 10x - x2 + 16
P = 8x2 + 14x + 32
P = 2( 4x2 + 7x + 16 )
DB
1
N
9 tháng 11 2018
\(A=\frac{x^2+4x+4}{x^2}\)
để A = 0 => \(x^2+4x+4=0\)
\(x^2+4x+4=0\Rightarrow x^2+2x+2x+4=0\)
\(\Rightarrow x.\left(x+2\right)+2.\left(x+2\right)=0\)
\(\left(x+2\right)^2=0\Rightarrow x+2=0\Rightarrow x=-2\)
vậy để A=0 => x=-2
TN
16 tháng 7 2018
\(4x^2-4x-35\) \(=\left(2x\right)^2-2.2x.1+1-36\)
\(=\left(2x-1\right)^2-6^2\)
\(=\left(2x-7\right)\left(2x+5\right)\)
\(18x^2-5x-2\) \(=\left(x-\frac{1}{2}\right)\left(x+\frac{2}{9}\right)\)
\(8x^3-26x^2+13x+5=\) \(8x^3-8x^2-18x^2+18x-5x+5\)
\(=8x^2\left(x-1\right)-18x\left(x-1\right)-5\left(x-1\right)\)
\(=\) \(\left(8x^2-18x-5\right)\left(x-1\right)\)
\(=\left(x-\frac{5}{2}\right)\left(x+\frac{1}{4}\right)\)\(\left(x-1\right)\)
8 tháng 11 2021
a) \(=x^2+2x-2x=x^2\)
b) \(=4-x^2+x^2=4\)
c) \(=x^2-x^3+x^3+27=x^2+27\)
d) \(=4x^2+4xy+y^2+4x^2-8x^2-4xy=y^2\)