Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1:
a: \(=\sqrt{\dfrac{7-4\sqrt{3}}{2-\sqrt{3}}}\cdot\sqrt{2+\sqrt{3}}\)
\(=\sqrt{2-\sqrt{3}}\cdot\sqrt{2+\sqrt{3}}=1\)
Bài 2:
\(VT=\left(4+\sqrt{15}\right)\cdot\left(\sqrt{5}-\sqrt{3}\right)\cdot\sqrt{8-2\sqrt{15}}\)
\(=\left(4+\sqrt{15}\right)\left(8-2\sqrt{15}\right)\)
\(=32-8\sqrt{15}+8\sqrt{15}-30=2\)

a: Ta có: \(A=\left(\dfrac{1}{\sqrt{x}+2}+\dfrac{1}{\sqrt{x}-2}\right)\cdot\dfrac{x-4}{3\sqrt{x}}\)
\(=\dfrac{\sqrt{x}-2+\sqrt{x}+2}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\cdot\dfrac{x-4}{3\sqrt{x}}\)
\(=\dfrac{2}{3}\)

a) Ta có: \(\sqrt{27\cdot48\left(1-a^2\right)}\)
\(=\sqrt{3^4\cdot4^2\cdot\left(1-a^2\right)}\)
\(=36\sqrt{1-a^2}\)
c) Ta có: \(\sqrt{5a}\cdot\sqrt{45a}-3a\)
\(=15a-3a=12a\)
b) Ta có: \(B=\dfrac{1}{a-b}\cdot\sqrt{a^4\cdot\left(a-b\right)^2}\)
\(=\dfrac{1}{a-b}\cdot a^2\cdot\left(a-b\right)\)
\(=a^2\)
d) Ta có: \(D=\left(3-a\right)^2-\sqrt{0.2}\cdot\sqrt{180a^2}\)
\(=a^2-6a+9-\sqrt{36a^2}\)
\(=a^2-6a+9-\left|6a\right|\)
\(=\left[{}\begin{matrix}a^2-6a+9-6a\left(a\ge0\right)\\a^2-6a+9+6a\left(a< 0\right)\end{matrix}\right.\)
\(=\left[{}\begin{matrix}a^2-12a+9\\a^2+9\end{matrix}\right.\)

a) =
= 0,6.│a│
Vì a < 0 nên │a│= -a. Do đó = -0,6a.
b) =
.
= │
│.│3 - a│.
Vì ≥ 0 nên │b│=
. Vì a ≥ 3 nên 3 - a ≤ 0, do đó │3 - a│= a - 3.
Vậy =
(a - 3).
c) =
=
= √81.√16.
= 9.4.│1 - a│
Vì a > 1 nên 1 - a < 0. Do đó │1 - a│= a -1.
Vậy = 36(a - 1).
d) :
=
: (
=
: (
.│a - b│)
Vì a > b nên a -b > 0, do đó│a - b│= a - b.
Vậy :
=
: (
(a - b)) =
.
a) =
= 0,6.│a│
Vì a < 0 nên │a│= -a. Do đó = -0,6a.
b) =
.
= │
│.│3 - a│.
Vì ≥ 0 nên │b│=
. Vì a ≥ 3 nên 3 - a ≤ 0, do đó │3 - a│= a - 3.
Vậy =
(a - 3).
c) =
=
= √81.√16.
= 9.4.│1 - a│
Vì a > 1 nên 1 - a < 0. Do đó │1 - a│= a -1.
Vậy = 36(a - 1).
d) :
=
: (
=
: (
.│a - b│)
Vì a > b nên a -b > 0, do đó│a - b│= a - b.
Vậy :
=
: (
(a - b)) =
.

\(A=\left|2-\sqrt{7}\right|+7-2\sqrt{7}+1\)
\(=\sqrt{7}-2+8-2\sqrt{7}\) \(=6-\sqrt{7}\)
\(B=3\cdot1,5-4\cdot\left|3-\sqrt{2}\right|\) \(=4,5-4\left(3-\sqrt{2}\right)\)
\(=4,5-12+4\sqrt{2}\) \(=4\sqrt{2}-7,5\)
Ta có: \(A=\sqrt{\left(2-\sqrt{7}\right)^2}+\left(\sqrt{7}-1\right)^2\)
\(=\sqrt{7}-2+8-2\sqrt{7}\)
\(=6-\sqrt{7}\)

a) \(\sqrt{\left(2-\sqrt{3}\right)^2}+\sqrt{7+4\sqrt{3}}=\left|2-\sqrt{3}\right|+\sqrt{4+4\sqrt{3}+3}\)
\(=2-\sqrt{3}+\sqrt{\left(2+\sqrt{3}\right)^2}=2-\sqrt{3}+\left|2+\sqrt{3}\right|\)
\(=2-\sqrt{3}+2+\sqrt{3}=4\)
b) \(\left(\frac{a\sqrt{a}+b\sqrt{b}}{\sqrt{a}+\sqrt{b}}-\sqrt{ab}\right):\left(a-b\right)+\frac{2\sqrt{b}}{\sqrt{a}+\sqrt{b}}\)
\(=\left[\frac{\left(\sqrt{a}\right)^3+\left(\sqrt{b}\right)^3}{\sqrt{a}+\sqrt{b}}-\sqrt{ab}\right].\frac{1}{a-b}+\frac{2\sqrt{b}}{\sqrt{a}+\sqrt{b}}\)
\(=\left[\frac{\left(\sqrt{a}+\sqrt{b}\right)\left(a-\sqrt{ab}+b\right)}{\sqrt{a}+\sqrt{b}}-\sqrt{ab}\right].\frac{1}{a-b}+\frac{2\sqrt{b}}{\sqrt{a}+\sqrt{b}}\)
\(=\left(a-\sqrt{ab}+b-\sqrt{ab}\right).\frac{1}{\left(\sqrt{a}-\sqrt{b}\right)\left(\sqrt{a}+\sqrt{b}\right)}+\frac{2\sqrt{b}}{\sqrt{a}+\sqrt{b}}\)
\(=\frac{\left(a-2\sqrt{ab}+b\right)}{\left(\sqrt{a}-\sqrt{b}\right)\left(\sqrt{a}+\sqrt{b}\right)}+\frac{2\sqrt{b}}{\sqrt{a}+\sqrt{b}}\)
\(=\frac{\left(\sqrt{a}-\sqrt{b}\right)^2}{\left(\sqrt{a}-\sqrt{b}\right)\left(\sqrt{a}+\sqrt{b}\right)}+\frac{2\sqrt{b}}{\sqrt{a}+\sqrt{b}}\)
\(=\frac{\sqrt{a}-\sqrt{b}}{\sqrt{a}+\sqrt{b}}+\frac{2\sqrt{b}}{\sqrt{a}+\sqrt{b}}=\frac{\sqrt{a}-\sqrt{b}+2\sqrt{b}}{\sqrt{a}+\sqrt{b}}\)
\(=\frac{\sqrt{a}+\sqrt{b}}{\sqrt{a}+\sqrt{b}}=1\)
a) \(\sqrt{\left(2-\sqrt{3}\right)^2}+\sqrt{7+4\sqrt{3}}\)
\(=\left|2-\sqrt{3}\right|+\sqrt{3+4\sqrt{3}+4}\)
\(=2-\sqrt{3}+\sqrt{\left(\sqrt{3}+2\right)^2}\)
\(=2-\sqrt{3}+\left|\sqrt{3}+2\right|\)
\(=2-\sqrt{3}+\sqrt{3}+2\)
\(=4\)
b) \(\left(\frac{a\sqrt{a}+b\sqrt{b}}{\sqrt{a}+\sqrt{b}}-\sqrt{ab}\right)\div\left(a-b\right)+\frac{2\sqrt{b}}{\sqrt{a}+\sqrt{b}}\)( \(\hept{\begin{cases}a,b\ge0\\a\ne b\end{cases}}\))
\(=\left(\frac{\left(\sqrt{a}+\sqrt{b}\right)\left(a-\sqrt{ab}+b\right)}{\left(\sqrt{a}+\sqrt{b}\right)}-\sqrt{ab}\right)\div\left(a-b\right)+\frac{2\sqrt{b}}{\sqrt{a}+\sqrt{b}}\)
\(=\left(a-\sqrt{ab}+b-\sqrt{ab}\right)\div\left(a-b\right)+\frac{2\sqrt{b}}{\sqrt{a}+\sqrt{b}}\)
\(=\left(a-2\sqrt{ab}+b\right)\div\left(a-b\right)+\frac{2\sqrt{b}}{\sqrt{a}+\sqrt{b}}\)
\(=\frac{a-2\sqrt{ab}+b}{a-b}+\frac{2\sqrt{b}}{\sqrt{a}+\sqrt{b}}\)
\(=\frac{a-2\sqrt{ab}+b}{\left(\sqrt{a}-\sqrt{b}\right)\left(\sqrt{a}+\sqrt{b}\right)}+\frac{2\sqrt{b}\left(\sqrt{a}-\sqrt{b}\right)}{\left(\sqrt{a}-\sqrt{b}\right)\left(\sqrt{a}+\sqrt{b}\right)}\)
\(=\frac{a-2\sqrt{ab}+b+2\sqrt{ab}-2b}{\left(\sqrt{a}-\sqrt{b}\right)\left(\sqrt{a}+\sqrt{b}\right)}\)
\(=\frac{a-b}{a-b}=1\)
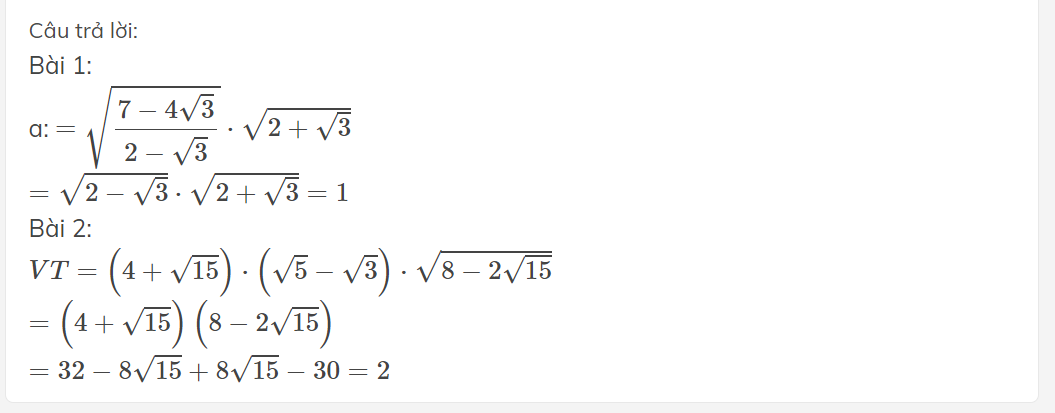
a/ \(=\sqrt{36^2\left(1-a\right)^2}=36.\left|1-a\right|=36\left(a-1\right)=36a-36\)
b/ \(=\frac{1}{a-b}.a^2\left|a-b\right|=\frac{1}{a-b}.a^2\left(a-b\right)=a^2\)
c/ \(=\frac{\sqrt{8+2\sqrt{7}}}{\sqrt{2}}+\frac{\sqrt{8-2\sqrt{7}}}{\sqrt{2}}=\frac{\sqrt{\left(\sqrt{7}+1\right)^2}+\sqrt{\left(\sqrt{7}-1\right)^2}}{\sqrt{2}}=\frac{\sqrt{7}+1+\sqrt{7}-1}{\sqrt{2}}=\frac{2\sqrt{7}}{\sqrt{2}}=\sqrt{14}\)