HT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
22 tháng 11 2021
\(a,A=\dfrac{3x+2-3x+2+3x-6}{\left(3x-2\right)\left(3x+2\right)}=\dfrac{3x-2}{\left(3x-2\right)\left(3x+2\right)}=\dfrac{1}{3x+2}\\ b,B=\dfrac{1}{2}+\dfrac{x}{\dfrac{x+2-x}{x+2}}=\dfrac{1}{2}+\dfrac{x}{\dfrac{2}{x+2}}=\dfrac{1}{2}+\dfrac{x\left(x+2\right)}{2}\\ B=\dfrac{1+x^2+2x}{2}=\dfrac{\left(x+1\right)^2}{2}\)
XO
21 tháng 8 2023
ĐKXĐ : \(x\ne0;x\ne\pm1\)
a) Bạn ghi lại rõ đề.
b) \(B=\dfrac{x-1}{x+1}+\dfrac{3x-x^2}{x^2-1}=\dfrac{x-1}{x+1}+\dfrac{3x-x^2}{\left(x-1\right).\left(x+1\right)}\)
\(=\dfrac{\left(x-1\right)^2+3x-x^2}{\left(x-1\right).\left(x+1\right)}=\dfrac{x+1}{\left(x-1\right).\left(x+1\right)}=\dfrac{1}{x-1}\)
c) \(P=A.B=\dfrac{x^2+x-2}{x.\left(x-1\right)}=\dfrac{\left(x-1\right).\left(x+2\right)}{x\left(x-1\right)}=\dfrac{x+2}{x}=1+\dfrac{2}{x}\)
Không tồn tại Min P \(\forall x\inℝ\)
2 tháng 7 2023
Sửa đề: 3x+căn 9x-3
\(P=\dfrac{3x+3\sqrt{x}-3-x+1-x+4}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{x+3\sqrt{x}+2}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}=\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\)
P=3
=>căn x+1=3căn x-3
=>-2căn x=-4
=>x=4
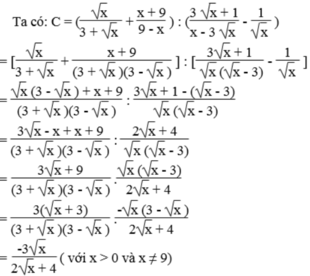
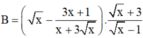
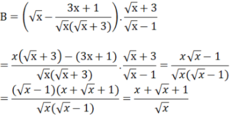
\(\left(x-1\right)^3+3\left(x-1\right)^2\cdot x+3\left(x-1\right)\cdot x^2+x^3\)
\(=\left(x-1+x\right)^3\)
\(=\left(2x-1\right)^3\)