K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
23 tháng 8 2021
hôm qua mình làm B rồi nhé
\(P=\left(\frac{1}{\sqrt{x}}+\frac{\sqrt{x}}{\sqrt{x}+1}\right):\frac{\sqrt{x}}{x+\sqrt{x}}\)ĐK : x > 0
\(=\frac{x+\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}+1\right)}:\frac{\sqrt{x}}{x+\sqrt{x}}=\sqrt{x}+1+\frac{1}{\sqrt{x}}\)
\(P=\frac{\sqrt{x}}{\sqrt{x}-1}+\frac{3}{\sqrt{x}+1}-\frac{6\sqrt{x}-4}{x-1}\)Với x >= 0 ; \(x\ne1\)
\(=\frac{x+\sqrt{x}+3\sqrt{x}-3-6\sqrt{x}+4}{x-1}=\frac{x-2\sqrt{x}+1}{x-1}=\frac{\sqrt{x}-1}{\sqrt{x}+1}\)
NT
3
31 tháng 8 2021
hình 1 : cho tam giác ABC vuông tại A, hạ đường cao AH, H thuộc BC
Xét tam giác ABC vuông tại A, đường AH
* Áp dụng hệ thức : \(AB^2=BH.BC\Rightarrow BH=y=\frac{AB^2}{BC}=\frac{225}{17}\)cm
=> \(CH=x=BC-y=17-\frac{225}{17}=\frac{64}{17}\)cm
* Áp dụng hệ thức : \(AC^2=c=CH.BC=\frac{64}{17}.17=64\Rightarrow AC=8\)cm
* Áp dụng hệ thức : \(AH.BC=AB.AC\Rightarrow AH=h=\frac{AB.AC}{BC}=\frac{15.8}{17}=\frac{120}{17}\)cm
tương tự hình 2 ; 3
1 tháng 9 2021
làm ko làm nốt luôn đi
dùng đã bt rồi nhưng cần kết quả để so sánh sai ở đâu
NT
3
3 tháng 9 2021
Bài 2a
Xét tam giác ABC vuông tại A, đường cao AH
* Áp dụng hệ thức : \(AH^2=BH.CH\Rightarrow CH=\frac{AH^2}{BH}=\frac{256}{25}\)cm
-> BC = HB + CH = \(25+\frac{256}{25}=\frac{881}{25}\)cm
Áp dụng định lí Pytago của tam giác ABH vuông tại H
\(AB=\sqrt{AH^2+HB^2}=\sqrt{881}\)cm
Áp dụng định lí Pytago tam giác ABC vuông tại A
\(AC=\sqrt{BC^2-AB^2}=18,9...\)cm
3 tháng 9 2021
Bài 2c
Xét tam giác ABC vuông tại A, đường cao AH
* Áp dụng hệ thức :
\(AH^2=HB.HC=3.4=12\Rightarrow AH=2\sqrt{3}\)cm
Theo định lí Pytago tam giác AHB vuông tại H
\(AB=\sqrt{AH^2+HB^2}=\sqrt{21}\)cm
* Áp dụng hệ thức : \(\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AC^2}\Rightarrow\frac{1}{12}=\frac{1}{21}+\frac{1}{AC^2}\Rightarrow AC=2\sqrt{7}\)cm
NT
2
22 tháng 8 2021
a, Thay x = vào A ta được : \(A=\frac{3}{3-2}=3\)
b, Với \(x\ge0;x\ne4\)
\(B=\frac{3}{\sqrt{x}+2}+\frac{\sqrt{x}}{\sqrt{x}-2}-\frac{\sqrt{x}-10}{x-4}\)
\(=\frac{3\sqrt{x}-6+x+2\sqrt{x}-\sqrt{x}+10}{x-4}=\frac{4\sqrt{x}+4+x}{x-4}\)
\(=\frac{\left(\sqrt{x}+2\right)^2}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}=\frac{\sqrt{x}+2}{\sqrt{x}-2}\)(đpcm)
8 tháng 6 2017
a) xét (o) ta có : BDC = 90 (góc nội tiếp chắng nữa (o))
\(\Rightarrow\) BD \(\perp\) AC
BEC = 90 (góc nội tiếp chắng nữa (o))
\(\Rightarrow\) CE \(\perp\) AB
xét \(\Delta\) ABC ta có : BD \(\perp\) AC (chứng minh trên)
CE \(\perp\) AB (chứng minh trên)
\(\Rightarrow\) H là trực tâm \(\Rightarrow\) AF \(\perp\) BC (đpcm)
\(\Rightarrow\) AFC = 90
ta có : EBD = ECD (2 góc nội tiếp cùng chắng cung ED của (o))
xét tứ giác ABDF ta có : ADB = 90 (kề bù góc BDC)
AFB = 90 (kề bù góc AFC)
mà 2 góc này cùng nhìn xuống BA \(\Rightarrow\) tứ giác ABDF nội tiếp
\(\Rightarrow\) ABD = AFD (2 góc nội tiếp cùng chắng cung AD của tứ giác ABDF)
\(\Leftrightarrow\) EBD = AFD
mà EBD = ECD
\(\Rightarrow\) AFD = ECD
\(\Leftrightarrow\) AFD = ACE (ĐPCM)
HA
7 tháng 9 2015
\(\frac{a\left(a-1\right)}{a-1}-\frac{a\left(-6a+5\right)}{a-1}=\frac{a^2-a+6a^2-5a}{a-1}\)
=\(\frac{7a^2-6a}{a-1}\)
NV
Nguyễn Việt Lâm
Giáo viên
27 tháng 7 2021
Gọi O là tâm đường tròn \(\Rightarrow\) O là trung điểm BC
\(\stackrel\frown{BE}=\stackrel\frown{ED}=\stackrel\frown{DC}\Rightarrow\widehat{BOE}=\widehat{EOD}=\widehat{DOC}=\dfrac{180^0}{3}=60^0\)
Mà \(OD=OE=R\Rightarrow\Delta ODE\) đều
\(\Rightarrow ED=R\)
\(BN=NM=MC=\dfrac{2R}{3}\Rightarrow\dfrac{NM}{ED}=\dfrac{2}{3}\)
\(\stackrel\frown{BE}=\stackrel\frown{DC}\Rightarrow ED||BC\)
Áp dụng định lý talet:
\(\dfrac{AN}{AE}=\dfrac{MN}{ED}=\dfrac{2}{3}\Rightarrow\dfrac{EN}{AN}=\dfrac{1}{2}\)
\(\dfrac{ON}{BN}=\dfrac{OB-BN}{BN}=\dfrac{R-\dfrac{2R}{3}}{\dfrac{2R}{3}}=\dfrac{1}{2}\)
\(\Rightarrow\dfrac{EN}{AN}=\dfrac{ON}{BN}=\dfrac{1}{2}\) và \(\widehat{ENO}=\widehat{ANB}\) (đối đỉnh)
\(\Rightarrow\Delta ENO\sim ANB\left(c.g.c\right)\)
\(\Rightarrow\widehat{NBA}=\widehat{NOE}=60^0\)
Hoàn toàn tương tự, ta có \(\Delta MDO\sim\Delta MAC\Rightarrow\widehat{MCA}=\widehat{MOD}=60^0\)
\(\Rightarrow\Delta ABC\) đều
NT
0
19 tháng 8 2021
\(P=\left(\frac{1}{\sqrt{x}}+\frac{\sqrt{x}}{\sqrt{x}+1}\right):\frac{\sqrt{x}}{x+\sqrt{x}}\)ĐK : x > 0
\(=\left(\frac{\sqrt{x}+1+x}{\sqrt{x}\left(\sqrt{x}+1\right)}\right):\frac{1}{\sqrt{x}+1}=\frac{x+\sqrt{x}+1}{\sqrt{x}}\)
\(P=\frac{\sqrt{x}}{\sqrt{x}-1}+\frac{3}{\sqrt{x}+1}-\frac{6\sqrt{x}-4}{x-1}\)
\(=\frac{x+\sqrt{x}+3\sqrt{x}-3-6\sqrt{x}+4}{x-1}=\frac{x-2\sqrt{x}+1}{x-1}=\frac{\sqrt{x}-1}{\sqrt{x}+1}\)
22 tháng 8 2021
Với \(x\ge0;x\ne\pm16\)
\(B=\left(\frac{\sqrt{x}}{\sqrt{x}+4}+\frac{4}{\sqrt{x}-4}\right):\frac{x+16}{\sqrt{x}+2}\)
\(=\left(\frac{x-4\sqrt{x}+4\sqrt{x}+16}{x-16}\right):\frac{x+16}{\sqrt{x}-2}=\frac{\sqrt{x}-2}{x-16}\)
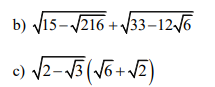
\(b,\sqrt{15-\sqrt{216}}+\sqrt{33-12\sqrt{6}}\\ =\sqrt{15-6\sqrt{6}}+\sqrt{\left(2\sqrt{6}-3\right)^2}\\ =\sqrt{\left(3-\sqrt{6}\right)^2}+2\sqrt{6}-3\\ =3-\sqrt{6}+2\sqrt{6}-3=\sqrt{6}\)
\(c,\sqrt{2-\sqrt{3}}\left(\sqrt{6}+\sqrt{2}\right)\\ =\sqrt{12-6\sqrt{3}}+\sqrt{4-2\sqrt{3}}\\ =\sqrt{\left(3-\sqrt{3}\right)^2}+\sqrt{\left(\sqrt{3}-1\right)^2}\\ =3-\sqrt{3}+\sqrt{3}-1=2\)
c: \(\sqrt{2-\sqrt{3}}\cdot\left(\sqrt{6}+\sqrt{2}\right)\)
\(=\sqrt{4-2\sqrt{3}}\cdot\left(\sqrt{3}+1\right)\)
\(=\left(\sqrt{3}-1\right)\left(\sqrt{3}+1\right)\)
=3-1
=2