Rút gọn biểu thức A = 3 8 - 18 + 5 1 2 + 50 ta được kết...

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn lớp

Chọn môn

Mua vip

Pham Trong Bach

22 tháng 5 2018

Rút gọn biểu thức A = 3 8 - 18 + 5 1 2 + 50 ta được kết quả là:

A. 21 2 2

B. 21 2

C. 11 2 2

D. 11 2

#Toán lớp 9

Cao Minh Tâm

22 tháng 5 2018

Đúng(0)

Các câu hỏi dưới đây có thể giống với câu hỏi trên

BBBT

26 tháng 8 2023

Thực hiện phép tính (rút gọn biểu thức)

a)\(\left(\sqrt{3}-2\right)\sqrt{7+4\sqrt{3}}\)

b) \(\sqrt{6+\sqrt{32}}\) - \(\sqrt{11-\sqrt{72}}\)

c) \(\sqrt{21-4\sqrt{5}}\) + \(\sqrt{21+4\sqrt{5}}\)

#Toán lớp 9

Nguyễn Lê Phước Thịnh

27 tháng 8 2023

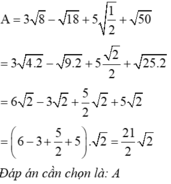
a: \(=\left(\sqrt{3}-2\right)\cdot\sqrt{\left(2+\sqrt{3}\right)^2}\)

\(=\left(\sqrt{3}-2\right)\left(\sqrt{3}+2\right)\)

=3-4=-1

b: \(=\sqrt{6+4\sqrt{2}}-\sqrt{11-2\sqrt{18}}\)

\(=\sqrt{\left(2+\sqrt{2}\right)^2}-\sqrt{\left(3-\sqrt{2}\right)^2}\)

\(=2+\sqrt{2}-3+\sqrt{2}=2\sqrt{2}-1\)

c: \(=\sqrt{\left(2\sqrt{5}-1\right)^2}+\sqrt{\left(2\sqrt{5}+1\right)^2}\)

\(=2\sqrt{5}-1+2\sqrt{5}+1\)

\(=4\sqrt{5}\)

Đúng(0)

Minh Joyce

1 tháng 8 2021

Câu 1Rút gọn biểu thức A = √24 + 2√54 - 2√96Câu 2Rút gọn biểu thức A = 3√48 + √75 - 2√108Câu 3Rút gọn biểu thức A = √18 - 2√50 + 3√8Câu 4Tính giá trị biểu thức A = √18 + 2√8 - \(\dfrac{1}{5}\)√50Câu 5 Rút gọn biểu thức M = √20 - √45 + √5Câu 6Tính giá trị biểu thức A = √5.(√5-3)...

Đọc tiếp

#Toán lớp 9

friknob

20 tháng 8 2021

1.
A= \(2\sqrt{6}\) + \(6\sqrt{6}\) - \(8\sqrt{6}\)
A= 0
2.
A= \(12\sqrt{3}\) + \(5\sqrt{3}\) - \(12\sqrt{3}\)
A= 0
3.
A= \(3\sqrt{2}\) - \(10\sqrt{2}\) + \(6\sqrt{2}\)
A= -\(\sqrt{2}\)
4.
A= \(3\sqrt{2}\) + \(4\sqrt{2}\) - \(\sqrt{2}\)
A= \(6\sqrt{2}\)
5.
M= \(2\sqrt{5}\) - \(3\sqrt{5}\) + \(\sqrt{5}\)
M= 0
6.
A= 5 - \(3\sqrt{5}\) + \(3\sqrt{5}\)
A= 5

This literally took me a while, pls sub :D
https://www.youtube.com/channel/UC4U1nfBvbS9y_Uu0UjsAyqA/featured

Đúng(0)

Louis louis

25 tháng 7 2018

Rút gọn biểu thức:

a.\(\left(2\sqrt{3}-\sqrt{5}\right).\sqrt{3}+\sqrt{60}\)

b.\(\left(\sqrt{28}-\sqrt{12}-\sqrt{7}\right).\sqrt{7}+2\sqrt{21}\)

c.\(\left(2\sqrt{5}+\sqrt{50}\right).\sqrt{5}-\sqrt{250}\)

d.\(\left(3\sqrt{11}-\sqrt{18}-\sqrt{11}\right).\sqrt{11}+3\sqrt{22}\)

#Toán lớp 9

Nguyễn Lê Phước Thịnh

7 tháng 8 2022

a: \(=6-\sqrt{15}+2\sqrt{15}=6+\sqrt{15}\)

b: \(=\left(\sqrt{7}-2\sqrt{3}\right)\cdot\sqrt{7}+2\sqrt{21}\)

\(=7-2\sqrt{21}+2\sqrt{21}=7\)

c: \(=10+5\sqrt{10}-5\sqrt{10}=10\)

d: \(=22-\sqrt{198}+\sqrt{198}=22\)

Đúng(0)

Sách Giáo Khoa

23 tháng 4 2017

Rút gọn các biểu thức :

a) \(\left(2\sqrt{3}+\sqrt{5}\right)\sqrt{3}-\sqrt{60}\)

b) \(\left(5\sqrt{2}+2\sqrt{5}\right)\sqrt{5}-\sqrt{250}\)

c) \(\left(\sqrt{28}-\sqrt{12}-\sqrt{7}\right)\sqrt{7}+2\sqrt{21}\)

d) \(\left(\sqrt{99}-\sqrt{18}-\sqrt{11}\right)\sqrt{11}+3\sqrt{22}\)

#Toán lớp 9

Mysterious Person

16 tháng 6 2017

a) \(\left(2\sqrt{3}+\sqrt{5}\right)\sqrt{3}-\sqrt{60}\) = \(6+\sqrt{15}-2\sqrt{15}\)

= \(6-\sqrt{15}\)

b) \(\left(5\sqrt{2}+2\sqrt{5}\right)\sqrt{5}-\sqrt{250}\) = \(5\sqrt{10}+10-5\sqrt{10}\) = \(10\)

c) \(\left(\sqrt{28}-\sqrt{12}-\sqrt{7}\right)\sqrt{7}+2\sqrt{21}\) = \(14-2\sqrt{21}-7+2\sqrt{21}\)

= \(7\)

d) \(\left(\sqrt{99}-\sqrt{18}-\sqrt{11}\right)\sqrt{11}+3\sqrt{22}\)

= \(33-3\sqrt{22}-11+3\sqrt{22}\) = \(22\)

Đúng(0)

Hoàng Hiếu

23 tháng 4 2017

a)(2√3+√5)√3-√60
=6+√15-2√15
=6-√15

b)(5√2+2√5)√5-√250
=5√10+10-5√10
=10

c)(√28-√12-√7)√7+2√21
=14-2√21-7+2√21
=7

d)(√99-√18-√11)√11+3√22
=33-3√22-11+3√22
=22

Đúng(0)

AK-47

16 tháng 7 2023

Rút gọn biểu thức

1)\(\sqrt{6+\sqrt{32}}\) - \(\sqrt{11-\sqrt{72}}\)

2) \(\sqrt{21-4\sqrt{5}}\) + \(\sqrt{21+4\sqrt{5}}\)

#Toán lớp 9

HT.Phong (9A5)

CTVHS

17 tháng 7 2023

1) \(\sqrt{6+4\sqrt{2}}-\sqrt{11-6\sqrt{2}}\)

\(=\sqrt{2^2+2\cdot2\cdot\sqrt{2}+\left(\sqrt{2}\right)^2}-\sqrt{3^2-2\cdot3\cdot\sqrt{2}+\left(\sqrt{2}\right)^2}\)

\(=\sqrt{\left(2+\sqrt{2}\right)^2}-\sqrt{\left(3-\sqrt{2}\right)^2}\)

\(=\left|2+\sqrt{2}\right|-\left|3-\sqrt{2}\right|\)

\(=2+\sqrt{2}-3+\sqrt{2}\)

\(=2\sqrt{2}-1\)

2) \(\sqrt{21-4\sqrt{5}}+\sqrt{21+4\sqrt{5}}\)

\(=\sqrt{20-4\sqrt{5}+1}+\sqrt{20+4\sqrt{5}+1}\)

\(=\sqrt{\left(2\sqrt{5}\right)^2-2\sqrt{5}\cdot2\cdot1+1^2}+\sqrt{\left(2\sqrt{5}\right)^2+2\sqrt{5}\cdot2\cdot1-1^2}\)

\(=\sqrt{\left(2\sqrt{5}-1\right)^2}+\sqrt{\left(2\sqrt{5}+1\right)^2}\)

\(=\left|2\sqrt{5}-1\right|+\left|2\sqrt{5}+1\right|\)

\(=2\sqrt{5}-1+2\sqrt{5}+1\)

\(=4\sqrt{5}\)

Đúng(0)

tamanh nguyen

1 tháng 12 2021

1) Rút gọn biểu thức \(\sqrt{0,81x^2}\) ta được kết quả là ....

2) Rút gọn \(\dfrac{\sqrt{63y^2}}{\sqrt{7y}}\) (với y < 0) ta được kết quả là ....

#Toán lớp 9

Nguyễn Hoàng Minh

1 tháng 12 2021

\(1,=0,9\left|x\right|\\ 2,Sửa:\dfrac{\sqrt{63y^3}}{\sqrt{7y}}=\sqrt{\dfrac{63y^3}{7y}}=\sqrt{9y^2}=3\left|y\right|=-3y\)

Đúng(1)

Cố Tư Thuần

8 tháng 5 2019

mọi người giúp em bài này với,em đang cần gấp ạ bài 2:rút gọn các biểu thức...

Đọc tiếp

#Toán lớp 9

Hoài Ngọc Phạm

8 tháng 5 2019

a, \(\sqrt{2}A=\sqrt{10-2\sqrt{3.7}}+\sqrt{10+2\sqrt{3.7}}\)
\(=\sqrt{\left(\sqrt{7}-\sqrt{3}\right)^2}+\sqrt{\left(\sqrt{3}+\sqrt{7}\right)^2}\)
\(=\left|\sqrt{7}-\sqrt{3}\right|+\left|\sqrt{7}+\sqrt{3}\right|\)
\(=\sqrt{7}-\sqrt{3}+\sqrt{3}+\sqrt{7}=2\sqrt{7}\)
\(\Rightarrow A=\sqrt{14}\)
b, \(B=\frac{\sqrt{5}\left(\sqrt{3}-1\right)}{\sqrt{3}-1}+\frac{\sqrt{5}\left(\sqrt{5}-2\right)}{2\left(\sqrt{5}-2\right)}\)
\(=\sqrt{5}+\frac{\sqrt{5}}{2}=\frac{3\sqrt{5}}{2}\)
c, \(C=\left(1-\sqrt{11}\right)\left(\sqrt{11}+1\right)=1-11=-10\)

d, \(D=\frac{\sqrt{2}\left(\sqrt{2}+\sqrt{3}\right)}{2-3}-\frac{\sqrt{2}\left(\sqrt{2}-\sqrt{3}\right)}{2-3}\)
\(=-2-\sqrt{6}+2-\sqrt{6}=-2\sqrt{6}\)

Đúng(0)

Lan Hoàng

31 tháng 10 2018

Rút gọn biểu thức

a, 3 căn 18 - căn 32 +4 căn 2 +căn 162

b, 2 căn 48 - 4 căn 27+ căn 75 + căn 12

c, căn 21+8 căn 5 + căn 21 -8 căn 5

d,(căn 14 - căn 7/căn 2-1 + căn 15 - căn 5/ căn 3-1 )÷1/căn 7- căn 5

#Toán lớp 9

Nguyễn Lê Phước Thịnh

15 tháng 11 2022

a: \(=9\sqrt{2}-4\sqrt{2}+4\sqrt{2}+9\sqrt{2}=18\sqrt{2}\)

b: \(=8\sqrt{3}-12\sqrt{3}+5\sqrt{3}+2\sqrt{3}=3\sqrt{3}\)

c: \(=2\sqrt{21}\)

Đúng(0)

Duyên Lê

15 tháng 7 2018 - olm

rút gọn biểu thức

a 3√5-2√125+√36

b √2- 2√8+4√32

c √15- 2√8 +√144X5

d ( √99- √18- √11 ) √11 +3 √22

giúp mình giải bài với ạ mình cảm ơn trước

#Toán lớp 9

Đỗ Minh Quang

21 tháng 11 2017 - olm

Rút gọn:

\(A=\sqrt{5-2\sqrt{3-\sqrt{3}}}-\sqrt{3+\sqrt{3}}+\sqrt{2+\sqrt{3}}\)

\(B=\frac{\sqrt{21+3\sqrt{5}}+\sqrt{21-3\sqrt{5}}}{\sqrt{21}+6\sqrt{11}}+\sqrt{11-6\sqrt{2}}\)

#Toán lớp 9

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP