Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Biểu thức này chỉ rút gọn được khi mẫu là \(1-2sin^210^0\)

Câu 3:
\(A=cos\frac{\pi}{7}.cos\frac{5\pi}{7}.cos\frac{4\pi}{7}=cos\frac{\pi}{7}.cos\left(\pi-\frac{2\pi}{7}\right).cos\frac{4\pi}{7}\)
\(A=-cos\frac{\pi}{7}.cos\frac{2\pi}{7}.cos\frac{4\pi}{7}\)
\(\Rightarrow sin\frac{\pi}{7}.A=-\frac{1}{2}.2sin\frac{\pi}{7}.cos\frac{\pi}{7}.cos\frac{2\pi}{7}.cos\frac{4\pi}{7}\)
\(\Rightarrow sin\frac{\pi}{7}.A=-\frac{1}{2}.sin\frac{2\pi}{7}.cos\frac{2\pi}{7}.cos\frac{4\pi}{7}\)
\(\Rightarrow sin\frac{\pi}{7}.A=-\frac{1}{4}sin\frac{4\pi}{7}.cos\frac{4\pi}{7}\)
\(\Rightarrow sin\frac{\pi}{7}.A=-\frac{1}{8}sin\frac{8\pi}{7}=-\frac{1}{8}sin\left(\pi+\frac{\pi}{7}\right)=\frac{1}{8}sin\frac{\pi}{7}\)
\(\Rightarrow A=\frac{1}{8}\)
Câu 4:
Đầu tiên ta chứng minh công thức:
\(tana+tanb=\frac{sina}{cosa}+\frac{sinb}{cosb}=\frac{sina.cosb+cosa.sinb}{cosa.cosb}=\frac{sin\left(a+b\right)}{cosa.cosb}\)
Áp dụng để biến đổi tử số:
\(tan30+tan60+tan40+tan50=\frac{sin90}{cos30.cos60}+\frac{sin90}{cos40.cos50}=\frac{1}{cos30.cos60}+\frac{1}{cos40.cos50}\)
\(=\frac{2}{cos90+cos30}+\frac{2}{cos90+cos10}=\frac{2}{cos30}+\frac{2}{cos10}=2\left(\frac{cos30+cos10}{cos30.cos10}\right)\)
\(=2\left(\frac{2cos20.cos10}{cos30.cos10}\right)=\frac{4.cos20}{cos30}=\frac{8\sqrt{3}}{3}.cos20\)
\(\Rightarrow A=\frac{\frac{8\sqrt{3}}{3}cos20}{cos20}=\frac{8\sqrt{3}}{3}\)
Câu 5:
\(cos54.cos4-cos36.cos86=cos54.cos4-cos\left(90-54\right).cos\left(90-4\right)\)
\(=cos54.cos4-sin54.sin4=cos\left(54+4\right)=cos58\)
Câu 1:
\(A=\frac{1}{2sin10}-2sin70=\frac{1-4sin10.sin70}{2sin10}=\frac{1+2\left(cos80-cos60\right)}{2sin10}\)
\(=\frac{1+2cos80-1}{2sin10}=\frac{2cos80}{2sin10}=\frac{sin10}{sin10}=1\)
Câu 2:
\(cos10.cos30.cos50.cos70=cos10.cos30.\frac{1}{2}\left(cos120+cos20\right)\)
\(=\frac{1}{2}cos30\left(cos10.cos120+cos10.cos20\right)\)
\(=\frac{1}{2}cos30\left(cos10.cos120+\frac{1}{2}\left(cos30+cos10\right)\right)\)
\(=\frac{1}{2}cos30\left(cos10.cos120+\frac{1}{2}cos30+\frac{1}{2}cos10\right)\)
\(=\frac{1}{2}.\frac{\sqrt{3}}{2}\left(-\frac{1}{2}cos10+\frac{1}{2}\frac{\sqrt{3}}{2}+\frac{1}{2}cos10\right)\)
\(=\frac{3}{16}\)

\(A = \sin {150^o} + \tan {135^o} + \cot {45^o}\)
Sử dụng bảng giá trị lượng giác của một số góc đặc biệt, ta có:
\(\sin {150^o} = \frac{1}{2};\tan {135^o} = - 1;\cot {45^o} = 1.\)
\( \Rightarrow A = \frac{1}{2} - 1 + 1 = \frac{1}{2}.\)
\(B = 2\cos {30^o} - 3\tan 150 + \cot {135^o}\)
Sử dụng bảng giá trị lượng giác của một số góc đặc biệt, ta có:
\(\cos {30^o} = \frac{{\sqrt 3 }}{2};\tan {150^o} = - \frac{{\sqrt 3 }}{3};\cot {135^o} = - 1.\)
\( \Rightarrow B = 2.\frac{{\sqrt 3 }}{2} - 3.\left( { - \frac{{\sqrt 3 }}{3}} \right) + 1 = 2\sqrt 3 + 1.\)

Ta có: \(\sin {70^o} = \cos {20^o};\;\cos {110^o} = - \cos {70^o} = - \sin {20^o}\)
\(\begin{array}{l} \Rightarrow A = {(\sin {20^o} + \cos {20^o})^2} + {(\cos {20^o} - \sin {20^o})^2}\\ = ({\sin ^2}{20^o} + {\cos ^2}{20^o} + 2\sin {20^o}\cos {20^o}) + ({\cos ^2}{20^o} + {\sin ^2}{20^o} - 2\sin {20^o}\cos {20^o})\\ = 2({\sin ^2}{20^o} + {\cos ^2}{20^o})\\ = 2\end{array}\)
Ta có: \(\tan {110^o} = - \tan {70^o} = - \cot {20^o};\;\cot {110^o} = - \cot {70^o} = - \tan {20^o}.\)
\( \Rightarrow B = \tan {20^o} + \cot {20^o} + ( - \cot {20^o}) + ( - \tan {20^o}) = 0\)

a)
Trên nửa đường tròn đơn vị, lấy điểm M sao cho \(\widehat {xOM} = \alpha \)
Gọi H, K lần lượt là các hình chiếu vuông góc của M trên Ox, Oy.
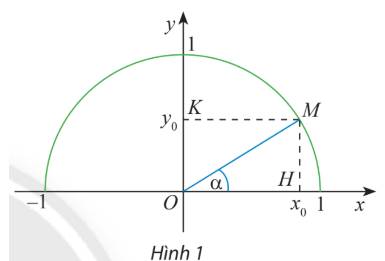
Ta có: tam giác vuông OHM vuông tại H và \(\alpha = \widehat {xOM}\)
Do đó: \(\sin \alpha = \frac{{MH}}{{OM}} = MH;\;\cos \alpha = \frac{{OH}}{{OM}} = OH.\)
\( \Rightarrow {\cos ^2}\alpha + {\sin ^2}\alpha = O{H^2} + M{H^2} = O{M^2} = 1\)
b) Ta có:
\(\begin{array}{l}\;\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }};\;\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }}.\\ \Rightarrow \;\tan \alpha .\cot \alpha = \frac{{\sin \alpha }}{{\cos \alpha }}.\frac{{\cos \alpha }}{{\sin \alpha }} = 1\end{array}\)
c) Với \(\alpha \ne {90^o}\) ta có:
\(\begin{array}{l}\;\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }};\;\\ \Rightarrow \;1 + {\tan ^2}\alpha = 1 + \frac{{{{\sin }^2}\alpha }}{{{{\cos }^2}\alpha }} = \frac{{{{\sin }^2}\alpha + {{\cos }^2}\alpha }}{{{{\cos }^2}\alpha }} = \frac{1}{{{{\cos }^2}\alpha }}\;\end{array}\)
d) Ta có:
\(\begin{array}{l}\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }};\;\\ \Rightarrow \;1 + {\cot ^2}\alpha = 1 + \frac{{{{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }} = \frac{{{{\sin }^2}\alpha + {{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }} = \frac{1}{{{{\sin }^2}\alpha }}\;\end{array}\)

Nhìn đề bài hãi quá :(
a/ \(A=3\sin\left(5.2\pi+\pi-x\right).\sin\left(2\pi+\frac{\pi}{2}-x\right)+2\sin\left(4.2\pi+\pi+x\right)\)
\(A=3\sin\left(\pi-x\right).\sin\left(\frac{\pi}{2}-x\right)+2\sin\left(\pi+x\right)\)
\(A=3\sin x.\cos x-2\sin x=\sin x\left(3\cos x-2\right)\)
b/ \(B=\sin\left(5.2.180^0+180^0+x\right)-\cos\left(90^0-x\right)+\tan\left(90^0+180^0-x\right)+\cot\left(2.180^0-x\right)\)
\(B=\sin\left(180^0+x\right)-\sin x+\tan\left(90^0-x\right)+\cot\left(-x\right)\)
\(B=-\sin x-\sin x+\cot x-\cot x=-2\sin x\)
c/ \(C=-2\sin\left(-(2\pi+\frac{\pi}{2}-x)\right)-3\cos\left(2\pi+\pi-x\right)+5\sin\left(2.2\pi-\left(\frac{\pi}{2}+x\right)\right)+\cot\left(\pi+\frac{\pi}{2}-x\right)\)
\(C=2\sin\left(\frac{\pi}{2}-x\right)-3\cos\left(\pi-x\right)-5\sin\left(\frac{\pi}{2}+x\right)+\cot\left(\frac{\pi}{2}-x\right)\)
\(2\cos x+3\cos x-5\cos x+\tan x=\tan x\)
d/ \(D=\tan\left(-\left(\pi-x\right)\right).\cos\left(-\left(\frac{\pi}{2}-x\right)\right).\left(-\cos x\right)\)
\(D=\tan\left(\pi-x\right).\cos\left(\frac{\pi}{2}-x\right).\cos x\)
\(D=-\tan x.\sin x.\cos x=-\sin^2x\)
e/ \(E=\cos\left(28.2\pi+\pi+\frac{\pi}{2}-x\right)+\sin\left(-\left(58.2\pi+\pi+\frac{\pi}{2}-x\right)\right)+\cos\left(-\left(46.2\pi+\pi+\frac{\pi}{2}-x\right)\right)+\sin\left(35.2\pi+\pi+\frac{\pi}{2}-x\right)\)
\(E=-\cos\left(\frac{\pi}{2}-x\right)+\sin\left(\frac{\pi}{2}-x\right)-\cos\left(\frac{\pi}{2}-x\right)-\sin\left(\frac{\pi}{2}-x\right)\)
\(E=-2\sin x\)
Thôi, stop ở đây, làm nữa chắc tẩu hỏa nhập ma quá :(
Mình thấy hầu hết các bài này đều có chung 1 điểm, và chắc đó cũng là điểm mà bạn thắc mắc: Đó chính là tách các hạng tử ra và biến đổi
Tách cũng đơn giản thôi, cứ gặp sin, cos thì tách sao cho về dạng 2pi+..., gặp tan, cot thì pi.
Còn tách mấy cái phân số như vầy:
Ví dụ \(\frac{7\pi}{2}\) , 7 chia 2 được 3, ta lấy \(\frac{7}{2}-3=\frac{1}{2}\) thì suy ra: \(\frac{7\pi}{2}=3\pi+\frac{\pi}{2}\)
Đó, thế là được :D

a: vect OA=(3;-1)
vecto OB=(4;2)
Vì 3/4<>-1/2
nên O,A,B ko thẳng hàng
b: OABM là hình bình hành
nên vecto OA=vecto MB
=>4-x=3 và 2-y=-1
=>x=1 và y=3
c: Tọa độ I là:
x=(3+4)/2=3,5 và y=(-1+2)/2=0,5

a) Ta có: \(\left\{ \begin{array}{l}\sin {100^o} = \sin \left( {{{180}^o} - {{80}^o}} \right) = \sin {80^o}\\\cos {164^o} = \cos \left( {{{180}^o} - {{16}^o}} \right) = - \cos {16^o}\end{array} \right.\)
\( \Rightarrow \sin {100^o} + \sin {80^o} + \cos {16^o} + \cos {164^o}\)\( = \sin {80^o} + \sin {80^o} + \cos {16^o}-\cos {16^o}\)\( = 2\sin {80^o}.\)
b)
Ta có:
\(\left\{ \begin{array}{l}\sin \left( {{{180}^o} - \alpha } \right) = \sin \alpha \\\cos \left( {{{180}^o} - \alpha } \right) = - \cos \alpha \\\tan \left( {{{180}^o} - \alpha } \right) = - \tan \alpha \\\cot \left( {{{180}^o} - \alpha } \right) = - \cot \alpha \end{array} \right.\quad ({0^o} < \alpha < {90^o})\)\( \Rightarrow 2\sin \left( {{{180}^o} - \alpha } \right).\cot \alpha - \cos \left( {{{180}^o} - \alpha } \right).\tan \alpha .\cot \left( {{{180}^o} - \alpha } \right)\) \( = 2\sin \alpha .\cot \alpha - \left( { - \cos \alpha } \right).\tan \alpha .\left( { - \cot \alpha } \right)\)\( = 2\sin \alpha .\cot \alpha - \cos \alpha .\tan \alpha .\cot \alpha \)
\( = 2\sin \alpha .\frac{{\cos \alpha }}{{\sin \alpha }} - \cos \alpha .\left( {\tan \alpha .\cot \alpha } \right)\)\( = 2\cos \alpha - \cos \alpha .1 = \cos \alpha .\)
\(A=\frac{sinx}{cosx}+\frac{cosx}{sinx}+\frac{sin3x}{cos3x}+\frac{cos3x}{sin3x}\)
\(=\frac{sin^2x+cos^2x}{sinx.cosx}+\frac{sin^23x+cos^23x}{sin3x.cos3x}=\frac{2}{2sinx.cosx}+\frac{2}{2sin3x.cos3x}\)
\(=\frac{2}{sin2x}+\frac{2}{sin6x}=\frac{2\left(sin2x+sin6x\right)}{sin2x.sin6x}=\frac{4sin4x.cos2x}{sin2x.sin6x}\)
\(=\frac{8sin2x.cos^22x}{sin2x.sin6x}=\frac{8cos^22x}{sin6x}\)
\(B=\frac{sin30}{cos30}+\frac{sin60}{cos60}+\frac{sin40}{cos40}+\frac{sin50}{cos50}=\frac{sin30.cos60+cos30.sin60}{cos30.cos60}+\frac{sin40.cos50+sin50.cos40}{cos40.cos50}\)
\(=\frac{sin90}{cos30.cos60}+\frac{sin90}{cos40.cos50}=\frac{1}{\frac{1}{2}.\frac{\sqrt{3}}{2}}+\frac{1}{\frac{1}{2}cos90+\frac{1}{2}cos10}\)
\(=\frac{4\sqrt{3}}{3}+\frac{2}{cos10}=\frac{4\sqrt{3}\left(cos10+\frac{\sqrt{3}}{2}\right)}{3cos10}=\frac{4\sqrt{3}\left(cos10+cos30\right)}{3cos10}\)
\(=\frac{8\sqrt{3}cos20.cos10}{3cos10}=\frac{8\sqrt{3}}{3}cos20\)