PT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
16 tháng 10 2019
MT1: x – y
MT2: 1
MTC: x – y
NTP1: 1; NTP2: x – y.
Quy đồng:
MB
1
22 tháng 1
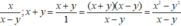
\(\dfrac{1}{3x+xy}=\dfrac{1}{x\left(y+3\right)}=\dfrac{\left(x+y\right)^2}{x\left(y+3\right)\left(x+y\right)^2}\)
\(2x+2y=2\left(x+y\right)=\dfrac{2\left(x+y\right)\cdot x\left(y+3\right)\left(x+y\right)^2}{x\left(y+3\right)\left(x+y\right)^2}\)
\(\dfrac{1}{x^2+2xy+y^2}=\dfrac{3x+xy}{x\left(y+3\right)\left(x+y\right)^2}\)
28 tháng 7 2023
a: 1/x^2y=1/x^2y
3/xy=3x/x^2y
b: \(\dfrac{x}{x^2+2xy+y^2}=\dfrac{x}{\left(x+y\right)^2}\)
\(\dfrac{2x}{x^2+xy}=\dfrac{2}{x+y}=\dfrac{2x+2y}{\left(x+y\right)^2}\)
M
1
28 tháng 7 2023
\(\dfrac{x^2-4}{x^2+2x}=\dfrac{\left(x-2\right)\left(x+2\right)}{x\left(x+2\right)}=\dfrac{x-2}{x}=\dfrac{\left(x-2\right)^2}{x\left(x-2\right)}\)
\(\dfrac{x}{x-2}=\dfrac{x^2}{x\left(x-2\right)}\)
MB
1
23 tháng 1
\(\dfrac{1}{3x+3y}=\dfrac{1}{3\left(x+y\right)}=\dfrac{2\cdot\left(x+y\right)}{6\left(x+y\right)^2}\)
\(\dfrac{1}{2x+2y}=\dfrac{1}{2\left(x+y\right)}=\dfrac{3\left(x+y\right)}{6\left(x+y\right)^2}\)
\(\dfrac{1}{x^2+2xy+y^2}=\dfrac{1}{\left(x+y\right)^2}=\dfrac{6}{6\left(x+y\right)^2}\)
PT
1
7 tháng 12 2021
Bài 2:
a: \(\dfrac{1}{2x^3y}=\dfrac{6yz^3}{12x^3y^2z^3}\)
\(\dfrac{2}{3xy^2z^3}=\dfrac{2\cdot4x^2}{12x^3y^2z^3}=\dfrac{8x^2}{12x^3y^2z^3}\)
HT
1
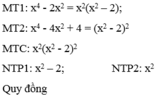
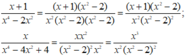
MTC: 5x(x – 2y);
NTP 1: x – 2y;
NTP2: 5x
Quy đồng: