Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: hệ số a=-2<0
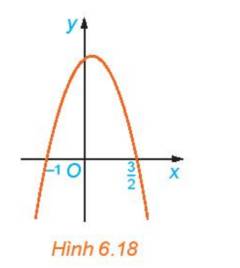
a) Nhìn vào đồ thị ta thấy
- Trên khoảng \(\left( { - \infty ; - 1} \right)\) đồ thị nằm phía dưới trục hoành
- Trên khoảng \(\left( { - 1;\frac{3}{2}} \right)\), đồ thị nằm phía trên trục hoành
- Trên khoảng \(\left( {\frac{3}{2}; + \infty } \right)\), đồ thị nằm phía dưới trục hoành
c) - Trên khoảng \(\left( { - \infty ; - 1} \right)\) đồ thị nằm phía dưới trục hoành => f(x)<0, cùng dầu với hệ số a
- Trên khoảng \(\left( { - 1;\frac{3}{2}} \right)\), đồ thị nằm phía trên trục hoành => f(x) >0, khác dấu với hệ số a
- Trên khoảng \(\left( {\frac{3}{2}; + \infty } \right)\), đồ thị nằm phía dưới trục hoành => f(x)<0, cùng dấu với hệ số a.

Đáp án :
B. Đồ thị hàm số chẵn nhận trục hoành làm trục đối xứng.

D sai, vì hệ số góc $a=1>0$, khi $x$ tăng (giảm) thì $y$ tương ứng tăng (giảm) nên hàm đồng biến trên $R$

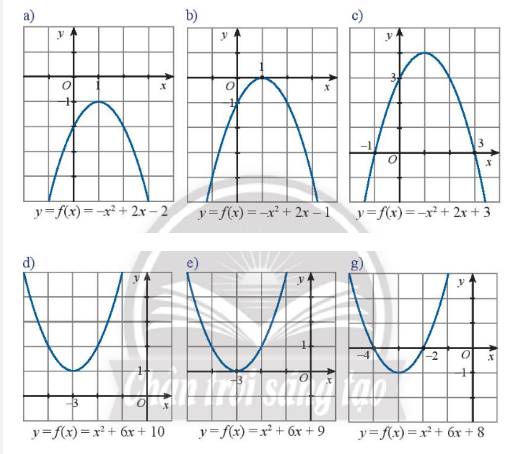
a) Dựa vào đồ thị ta thấy hàm số đã cho vô nghiệm
Biệt thức \(\Delta = {2^2} - 4.\left( { - 1} \right).\left( { - 2} \right) = - 4 < 0\)
Ta thấy hệ số của \({x^2}\) là \( - 1 < 0\)
Đồ thị nằm dưới trục hoành với mọi x
Nên \(f\left( x \right)\) cùng dấu với hệ số của \({x^2}\) với \(\forall x \in \mathbb{R}\)
b) Dựa vào đồ thị ta thấy hàm số đã cho có nghiệm kép \({x_1} = {x_2} = 1\)
Biệt thức \(\Delta = {2^2} - 4.\left( { - 1} \right).\left( { - 1} \right) = 0\)
Ta thấy hệ số của \({x^2}\) là \( - 1 < 0\)
Đồ thị nằm dưới trục hoành với mọi x
Nên \(f\left( x \right)\) cùng dấu với hệ số của \({x^2}\) với \(\forall x \in \mathbb{R}\)
c) Dựa vào đồ thị ta thấy hàm số đã cho có hai nghiệm phân biệt \({x_1} = - 1;{x_2} = 3\)
Biệt thức \(\Delta = {2^2} - 4.\left( { - 1} \right).3 = 16 > 0\)
Ta thấy hệ số của \({x^2}\) là \( - 1 < 0\)
Đồ thị nằm dưới trục hoành khi \(x \in \left( { - \infty , - 1} \right) \cup \left( {3, + \infty } \right)\)
Đồ thị nằm trên trục hoành với mọi \(x \in \left( { - 1,3} \right)\)
Nên \(f\left( x \right)\) cùng dấu với hệ số của \({x^2}\) khi \(x \in \left( { - \infty , - 1} \right) \cup \left( {3, + \infty } \right)\)
d) Dựa vào đồ thị ta thấy hàm số bậc hai đã cho vô nghiệm
Biệt thức \(\Delta = {6^2} - 4.1.10 = - 4 < 0\)
Ta thấy hệ số của \({x^2}\) là \(1 > 0\)
Đồ thị nằm trên trục hoành với mọi \(x\)
Nên \(f\left( x \right)\) cùng dấu với hệ số của \({x^2}\) với mọi \(x \in \mathbb{R}\)
e) Dựa vào đồ thị ta thấy hàm số đã cho có nghiệm kép \({x_1} = {x_2} = - 3\)
Biệt thức \(\Delta = {6^2} - 4.1.9 = 0\)
Ta thấy hệ số của \({x^2}\) là \(1 > 0\)
Đồ thị nằm trên trục hoành với mọi x
Nên \(f\left( x \right)\) cùng dấu với hệ số của \({x^2}\) với mọi \(x \in \mathbb{R}\)
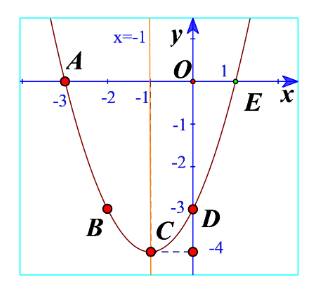
g) ) Dựa vào đồ thị ta thấy hàm số đã cho có hai nghiệm phân biệt \({x_1} = - 4;{x_2} = - 2\)
Biệt thức \(\Delta = {6^2} - 4.1.8 = 4 > 0\)
Ta thấy hệ số của \({x^2}\) là \(1 > 0\)
Đồ thị nằm trên trục hoành khi \(x \in \left( { - \infty , - 4} \right) \cup \left( { - 2, + \infty } \right)\)
Đồ thị nằm dưới trục hoành với mọi \(x \in \left( { - 4, - 2} \right)\)
Nên \(f\left( x \right)\) cùng dấu với hệ số của \({x^2}\) khi \(x \in \left( { - \infty , - 4} \right) \cup \left( { - 2, + \infty } \right)\)

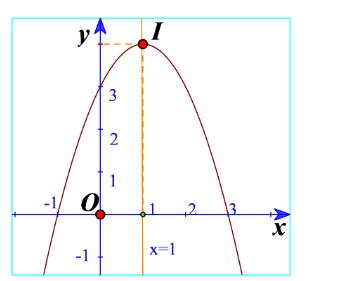
a) Từ đồ thị ta thấy đồ thị hàm số đi lên trong khoảng \(\left( { - 1; + \infty } \right)\) nên hàm số đồng biến trong khoảng \(\left( { - 1; + \infty } \right)\). Trong khoảng \(\left( { - \infty ; - 1} \right)\) thì hàm số nghich biến.
Bảng biến thiên:
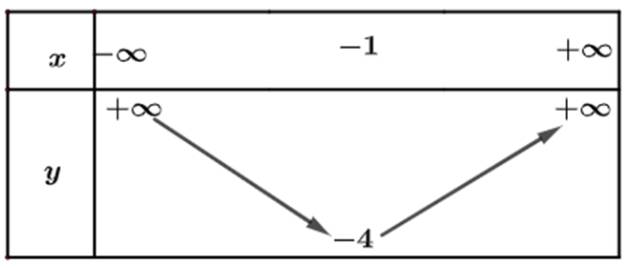
b) Từ đồ thị ta thấy đồ thị hàm số đi lên trong khoảng \(\left( { - \infty ;1} \right)\) nên hàm số đồng biến trong khoảng \(\left( { - \infty ;1} \right)\). Trong khoảng \(\left( {1; + \infty } \right)\) thì hàm số nghịch biến.
Bảng biến thiên:
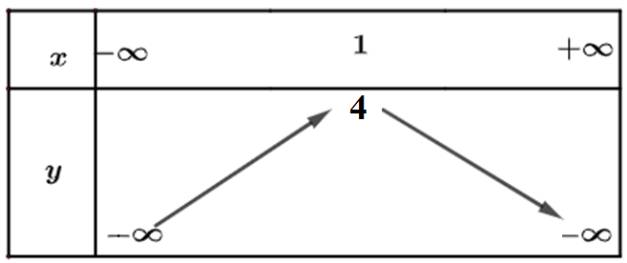

\(-x^2+4x-3=0\)
\(\Leftrightarrow\left[{}\begin{matrix}p=1\\q=3\end{matrix}\right.\)
\(p+2q=1+2\cdot3=7\)
PT giao điểm của đths và trục hoành là
\(y=0\Leftrightarrow x^2-4x+3=0\Leftrightarrow\left[{}\begin{matrix}x=1\\x=3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}p=1\\q=3\end{matrix}\right.\)
Do đó \(p+2q=1+6=7\)

Phương trình hoành độ giao điểm của (P ) và trục hoành:
x2+ 3x+m=0 (1)
+ Để đồ thị cắt trục hoành tại hai điểm phân biệt khi phương trình (1) có hai nghiệm phân biệt
![]()
Chọn D.

a) (P) nằm hoàn toàn trên trục hoành thì (P) không cắt trục hoành => Phương trình
\(a{x^2} + bx + c = 0\)vô nghiệm => \(\Delta < 0\)
(P) nằm hoàn toàn trên trục hoành thì bề lõm phải hướng lên trên => a>0
b) Tương tự câu a:
(P) nằm hoàn toàn dưới trục hoành thì (P) không cắt trục hoành => Phương trình \(a{x^2} + bx + c = 0\)vô nghiệm => \(\Delta < 0\)
(P) nằm hoàn toàn dưới trục hoành thì bề lõm phải hướng xuống dưới=> a<0
c) (P) cắt trục hoành tại hai điểm phân biệt => Phương trình \(a{x^2} + bx + c = 0\) có 2 nghiệm phân biệt=> \(\Delta > 0\)
(P) có đỉnh nằm phía dưới trục hoành mà có 2 nghiệm phân biệt thì bề lõm phải hướng lên trên ⇒ a>0
d) (P) tiếp xúc với trục hoành ⇒ Phương trình \(a{x^2} + bx + c = 0\)có duy nhất 1 nghiệm ⇒ \(\Delta = 0\)
(P) nằm phía trên trục hoành nên bề lõm phải hướng lên trên ⇒ a > 0
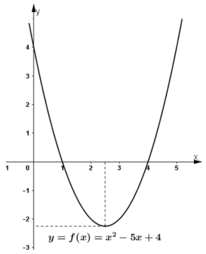
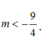
Với 1 < x < 4 thì đồ thị nằm phía dưới trục hoành.
Với x < 1 hoặc x > 4 thì đồ thị nằm phía trên trục hoành.