
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Số tổ hợp con có x phần tử là số tổ hợp chập x của 5.
=> Số tổ hợp con có lẻ phần tử là: \(C_5^1 + C_5^3 + C_5^5=5+10+1=16\)
Số tổ con có chẵn phần tử là: \(C_5^0 + C_5^2 + C_5^4=1+10+5=16\)
\( \Rightarrow C_5^0 + C_5^2 + C_5^4 = C_5^1 + C_5^3 + C_5^5\) (đpcm)

Tham khảo:
Ta có:
Mỗi hình chữ nhật là một hình bình hành đặc biệt (có một góc vuông). Do đó: \(C \subset B\)
Mỗi hình thoi là một hình bình hành đặc biệt (có hai cạnh kề bằng nhau). Do đó: \(E \subset B\)
Mỗi hình bình hành là một hình tứ giác (có một cặp cạnh đối song song và bằng nhau). Do đó: \(B \subset A\)
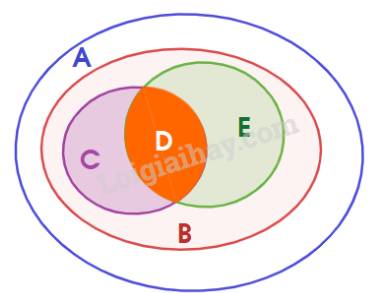
\(C \cap E\)là tập hợp các hình vừa là hình chữ nhật vừa là hình thoi, hay là hình chữ nhật có 4 cạnh bằng nhau (hình vuông). Do đó: \(C \cap E = D\)
Kết hợp lại ta có: \(\left\{ \begin{array}{l}D \subset C \subset B \subset A,\\D \subset E \subset B \subset A,\\C \cap E = D\end{array} \right.\)
Biểu đồ Ven:

\(A=\left\{-1;0;1\right\}\\ A\cap B=\left\{0;1\right\}\\ A\cup B=\left\{-1;0;1;2;3;4;5\right\}\)

- Vì hình vuông là hình chữ nhật nên E ⊂ D.
- Vì hình chữ nhật là hình bình hành nên D ⊂ B.
- Vì hình bình hành là hình thang nên B ⊂ C.
- Vì hình thang là hình tứ giác nên C ⊂ A.
Vậy E ⊂ D ⊂ B ⊂ C ⊂ A.
Mặt khác:
- Vì hình vuông là hình thoi nên E ⊂ G.
- Vì hình thoi là hình bình hành nên G ⊂ B.
Vậy E ⊂ G ⊂ B ⊂ C ⊂ A.

Gọi \(S=\left\{\overline{abc}\right\}\)
a có 5 cách chọn
b có 5 cách chọn
c có 4 cách chọn
=>S có 5*5*4=100 số
Gọi \(\overline{abc}\) là số chia hết cho 5
TH1: c=5
=>a có 4 cách và b có 4 cách
=>Có 16 cách
TH2: c=0
=>a có 5 cách và b có 4 cách
=>Có 5+4=20 cách
=>Có 16+20=36(cách)
\(n\left(\Omega\right)=C^2_{100}\)
\(n\left(B\right)=C^2_{36}\)
=>\(P\left(B\right)=\dfrac{7}{55}\)

Vì các học sinh tổ I đều là các học sinh lớp 10D nên tập hợp B là tập con của tập hợp A.
Kí hiệu: \(B \subset A\)

A = {x < 20 | x thuộc N}
= {1 ; 2 ; 3 ; ... ; 19}
B = {x lẻ | x khác 0}
= {1 ; 3 ; 5 ; 7 ; ...}
\(A\subset N\)
\(B\subset N\)
A= {X<20|x thuộc N }
= {1;2;3...;19}
B= { x lẻ |x khác 0}
= { 1;3:5:7,...}
A€ N
B€ N
\(B\subset C\)
\(A\subset C\)