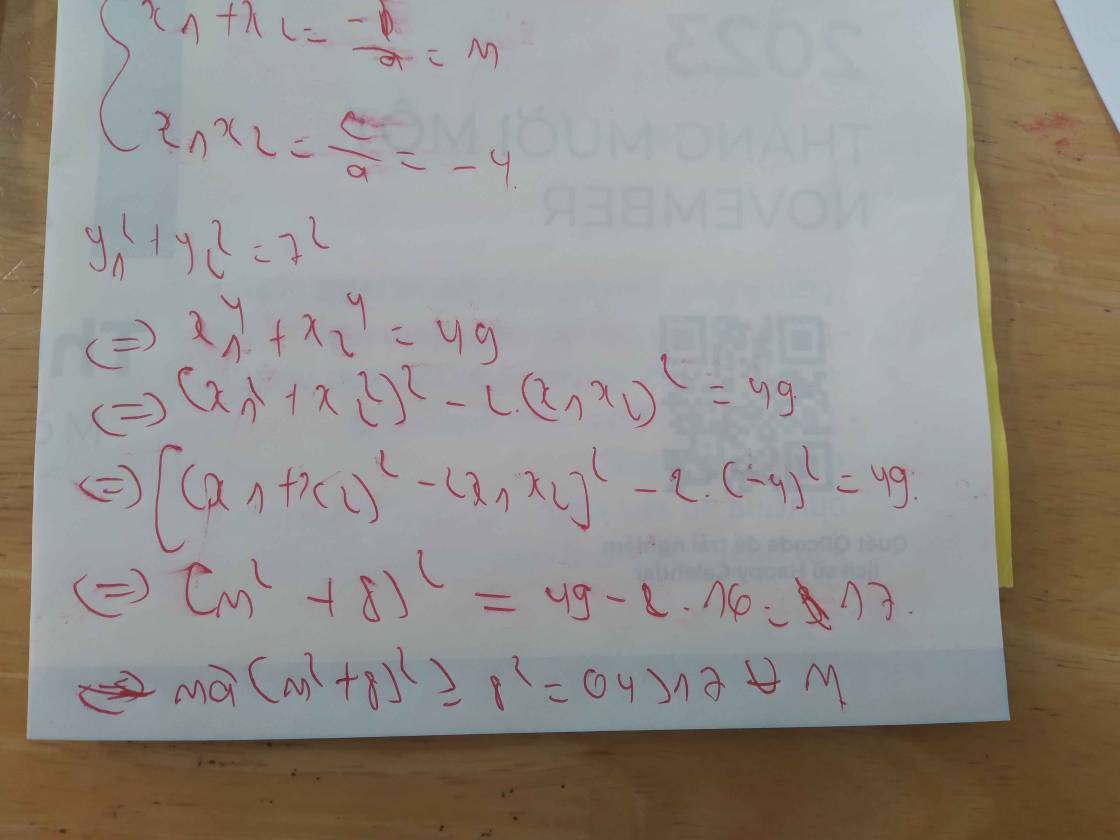Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: PTHĐGĐ là;
-1/4x^2-mx+m+2=0
=>1/4x^2+mx-m-2=0
=>x^2+4mx-4m-8=0
\(\text{Δ}=\left(4m\right)^2-4\left(-4m-8\right)\)
\(=16m^2+16m+32\)
\(=16m^2+2\cdot4m\cdot2+4+28=\left(4m+2\right)^2+28>0\)
=>Phương trình luôn có hai nghiệm phân biệt
b: \(A=x_1\cdot x_2\left(x_1+x_2\right)\)
\(=4m\left(4m+8\right)\)
\(=\left(16m^2+32m+16-16\right)\)
\(=\left(4m+4\right)^2-16>=-16\)
Dấu = xảy ra khi m=-1

a, Xét hoành độ giao điểm của P và d ta có:
x2 = 3x + m2 - 2
\(\Delta=b^2-4ac=4m^2+1>0\) ∀x
=> d luôn cắt P tại hai điểm phân biệt.

a: PTHĐGĐ là:
x^2+mx-m-2=0(1)
Khi m=2 thì (1) sẽ là
x^2+2x-2-2=0
=>x^2+2x-4=0
=>\(\left[{}\begin{matrix}x=-1+\sqrt{5}\\x=-1-\sqrt{5}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}y=6-2\sqrt{5}\\y=6+2\sqrt{5}\end{matrix}\right.\)
b: Δ=m^2-4(-m-2)
=m^2+4m+8
=(m+2)^2+4>0 với mọi x
=>(d) luôn cắt (P) tại hai điểm phân biệtx
x1^2+x2^2=7
=>(x1+x2)^2-2x1x2=7
=>(-m)^2-2(-m-2)=7
=>m^2+2m+4-7=0
=>m^2+2m-3=0
=>m=-3 hoặc m=1

xét phương trình hoành độ giao điểm
\(x^2-mx+m-1=0\Leftrightarrow\left(x-1\right)\left(x-m+1\right)=0\)
vậy khi m=-2 thì tọa độ hai giao điểm là \(\hept{\begin{cases}x=1,y=1\\x=-3,y=9\end{cases}}\)
b. ta có \(\left|x_1\right|+\left|x_2\right|=1+\left|m-1\right|=4\Leftrightarrow\left|m-1\right|=3\Leftrightarrow\orbr{\begin{cases}m=4\\m=-2\end{cases}}\)

Phương trình hoành độ giao điểm là:
\(x^2-3x-m^2+1=0\)
\(\text{Δ}=\left(-3\right)^2-4\left(-m^2+1\right)=4m^2-4+9=4m^2+5>0\)
Do đó: (P) luôn cắt (d) tại hai điểm phân biệt

a) Xét phương trình hoành độ giao điểm
\(x^2=-x+2\) \(\Leftrightarrow\left[{}\begin{matrix}x=1\Rightarrow y=1\\x=-2\Rightarrow y=4\end{matrix}\right.\)
Vậy tọa độ giao điểm là \(\left(1;1\right)\) và \(\left(-2;4\right)\)