Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1. Để xác định được tốc độ trung bình của viên bi khi đi từ cổng quang điện E đến cổng quang điện F ta cần:
- Xác định độ dài quãng đường s (chính là khoảng cách giữa 2 cổng quang điện E và F).
- Chỉnh đồng hồ đo về chế độ đo thời gian vật đi qua hai cổng quang chọn MODE A↔B (tức là vật bắt đầu đi vào cổng quang E thì đồng hồ bắt đầu chạy, khi vật đi qua cổng quang F thì đồng hồ dừng lại).
- Đo thời gian viên bi chuyển động từ cổng quang điện E đến cổng quang điện F.
- Sử dụng công thức \(v=\dfrac{s}{t}\) ta sẽ xác định được tốc độ trung bình của viên bi.
2. Để xác định được tốc độ tức thời của viên bi khi đi qua cổng quang điện E hoặc cổng quang điện F ta cần:
- Xác định được đường kính d của viên bi.
- Chỉnh chế độ đo thời gian của đồng hồ, chuyển về chế độ đo thời gian vật đi qua một cổng quang điện chọn MODE A hoặc MODE B (tức là vật bắt đầu đi vào cổng quang thì đồng hồ chạy số, sau khi vật đi qua cổng quang đó thì đồng hồ dừng lại).
- Xác định được thời gian viên bi chuyển động qua cổng quang điện E hoặc cổng quang điện F.
- Sử dụng công thức \(v=\dfrac{d}{t}\) ta sẽ xác định được tốc độ tức thời của viên bi.
3. Các yếu tố có thể gây sai số:
- Sai số của các dụng cụ đo.
- Thao tác bấm công tắc của người không dứt khoát.
- Cách đo, đọc giá trị quãng đường, đường kính viên bi của người làm thực hành chưa chính xác.
- Các yếu tố khách quan như gió, …
Cách để làm giảm sai số
- Tiến hành đo nhiều lần và lấy giá trị trung bình của các lần đo.
- Tắt hết quạt, điều hòa khi tiến hành thí nghiệm.

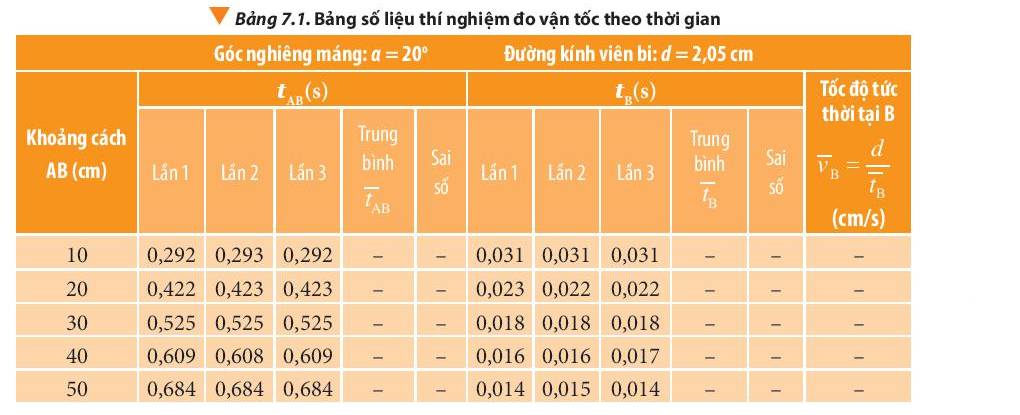
- Giá trị trung bình thời gian của viên bi chuyển động từ A đến B là:
+ AB = 10 cm: \(\overline t = \frac{{0,292 + 0,293 + 0,292}}{3} \approx 0,292(s)\)
+ AB = 20 cm: \(\overline t = \frac{{0,422 + 0,423 + 0,423}}{3} \approx 0,423(s)\)
+ AB = 30 cm: \(\overline t = \frac{{0,525 + 0,525 + 0,525}}{3} = 0,525(s)\)
+ AB = 40 cm: \(\overline t = \frac{{0,609 + 0,608 + 0,609}}{3} \approx 0,609(s)\)
+ AB = 50 cm: \(\overline t = \frac{{0,609 + 0,608 + 0,609}}{3} \approx 0,609(s)\)
- Sai số của phép đo thời gian viên bi chuyển động từ A đến B:
+ AB = 10 cm:
\(\begin{array}{l}\Delta {t_1} = \left| {0,292 - 0,292} \right| = 0\\\Delta {t_2} = \left| {0,293 - 0,292} \right| = 0,001\\\Delta {t_3} = \left| {0,292 - 0,292} \right| = 0\\ \Rightarrow \overline {\Delta t} = \frac{{0,001}}{3} \approx 3,{33.10^{ - 4}}(s)\end{array}\)
Tương tự cho các đoạn còn lại, ta có:
+ AB = 20 cm: \(\overline {\Delta t} = 3,{33.10^{ - 4}}(s)\)
+ AB = 30 cm: \(\overline {\Delta t} = 0\)
+ AB = 40 cm: \(\overline {\Delta t} = 3,{33.10^{ - 4}}(s)\)
+ AB = 50 cm: \(\overline {\Delta t} = 0\)
- Giá trị trung bình và sai số của thời gian chắn cổng quang điện tại B:
+ AB = 10 cm: \(\overline t = 0,031;\overline {\Delta t} = 0\)
+ AB = 20 cm: \(\overline t = 0,022;\overline {\Delta t} = 3,{33.10^{ - 4}}\)
+ AB = 30 cm: \(\overline t = 0,018;\overline {\Delta t} = 0\)
+ AB = 40 cm: \(\overline t = 0,016;\overline {\Delta t} = 3,{33.10^{ - 4}}\)
+ AB = 50 cm: \(\overline t = 0,014;\overline {\Delta t} = 3,{33.10^{ - 4}}\)
- Tốc độ tức thời tại B:
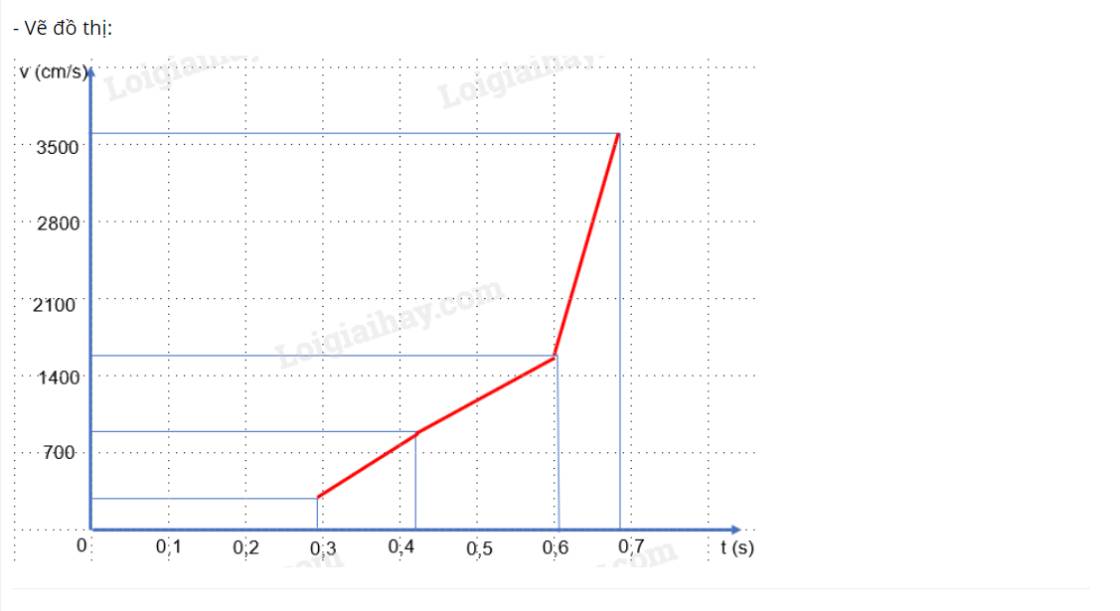
+ AB = 10 cm: \(\overline {{v_B}} = \frac{d}{{\overline {{t_B}} }} = \frac{{10}}{{0,031}} \approx 322,58(cm/s)\)
+ AB = 20 cm: \(\overline {{v_B}} = \frac{d}{{\overline {{t_B}} }} = \frac{{20}}{{0,022}} \approx 909,09(cm/s)\)
+ AB = 30 cm: \(\overline {{v_B}} = \frac{d}{{\overline {{t_B}} }} = \frac{{30}}{{0,018}} \approx 1666,67(cm/s)\)
+ AB = 40 cm: \(\overline {{v_B}} = \frac{d}{{\overline {{t_B}} }} = \frac{{40}}{{0,016}} = 2500(cm/s)\)
+ AB = 50 cm: \(\overline {{v_B}} = \frac{d}{{\overline {{t_B}} }} = \frac{{50}}{{0,014}} \approx 3571,43(cm/s)\)
- Vẽ đồ thị:
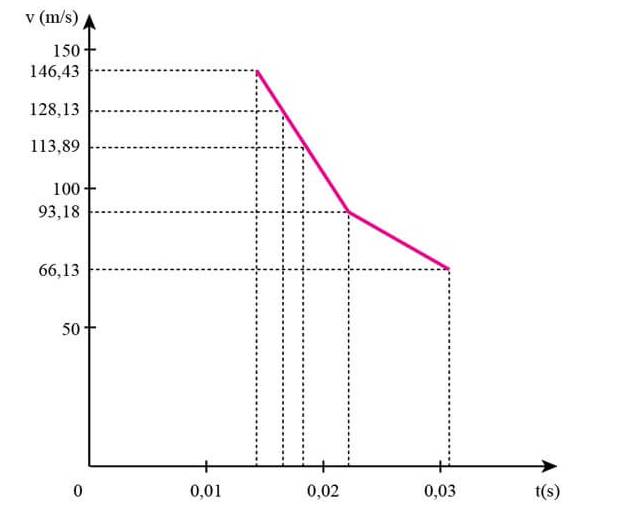

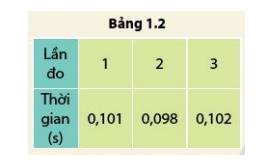
Thời gian trung bình của phép đo là:
\(\overline t = \frac{{{t_1} + {t_2} + {t_3}}}{3} = \frac{{0,101 + 0,098 + 0,102}}{3} \approx 0,100(s)\)
Sai số tuyệt đối trung bình của phép đo là:
\(\begin{array}{l}\Delta {t_1} = \left| {{t_2} - {t_1}} \right| = \left| {0,098 - 0,101} \right| = 0,003\\\Delta {t_2} = \left| {{t_3} - {t_2}} \right| = \left| {0,102 - 0,098} \right| = 0,004\\\overline {\Delta t} = \frac{{\Delta {t_1} + \Delta {t_2}}}{2} = \frac{{0,003 + 0,004}}{2} \approx 0,004(s)\end{array}\)

- Thiết kế phương án thí nghiệm đo tốc độ.
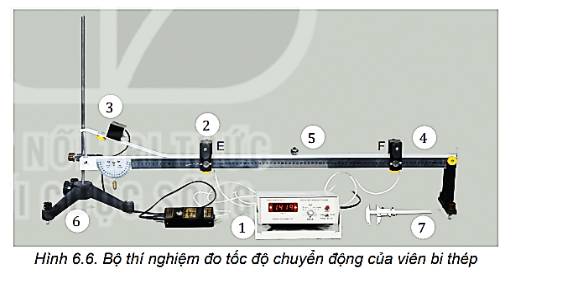
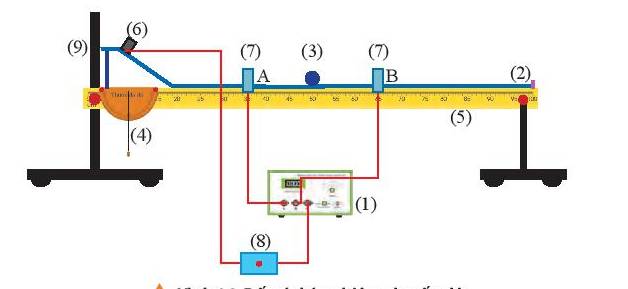
Bước 1: Bố trí thí nghiệm như hình 6.2. Điều chỉnh đoạn nằm ngang của máng sao cho thước đo độ chỉ 00 . Cố định nam châm điện và cổng quang điện A (đặt cách đoạn chân dốc nghiêng của máng một khoảng 20 cm).
Bước 2: Chọn MODE ở vị trí A (hoặc B) để đo thời gian viên bi chắn cổng quang điện mà ta muốn đo tốc độ tức thời của viên bi ở vị trí tương ứng.
Bước 3: Sử dụng thước kẹp để đo đường kính của viên bi. Thực hiện đo đường kính viên bi khoảng 5 lần và ghi kết quả.
Bước 4: Đưa viên bi lại gần nam châm điện sao cho viên bi hút vào nam châm. Ngắt công tắc điện để viên bi bắt đầu chuyển động xuống đoạn dốc nghiêng và đi qua cổng quang điện cần đo thời gian.
Bước 5: Ghi nhận giá trị thời gian hiển thị trên đồng hồ đo.
- Thực hiện phương án thí nghiệm
Học sinh tự thực hành.

- Thiết kế phương án thí nghiệm đo tốc độ.
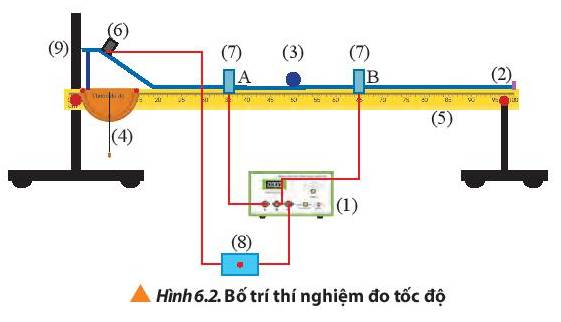
Bước 1: Bố trí thí nghiệm như hình 6.2. Điều chỉnh đoạn nằm ngang của máng sao cho thước đo độ chỉ 00 . Cố định nam châm điện và cổng quang điện A (đặt cách đoạn chân dốc nghiêng của máng một khoảng 20 cm).
Bước 2: Chọn MODE ở vị trí A (hoặc B) để đo thời gian viên bi chắn cổng quang điện mà ta muốn đo tốc độ tức thời của viên bi ở vị trí tương ứng.
Bước 3: Sử dụng thước kẹp để đo đường kính của viên bi. Thực hiện đo đường kính viên bi khoảng 5 lần và ghi kết quả.
Bước 4: Đưa viên bi lại gần nam châm điện sao cho viên bi hút vào nam châm. Ngắt công tắc điện để viên bi bắt đầu chuyển động xuống đoạn dốc nghiêng và đi qua cổng quang điện cần đo thời gian.
Bước 5: Ghi nhận giá trị thời gian hiển thị trên đồng hồ đo.
- Thực hiện phương án thí nghiệm
Học sinh tự thực hành.


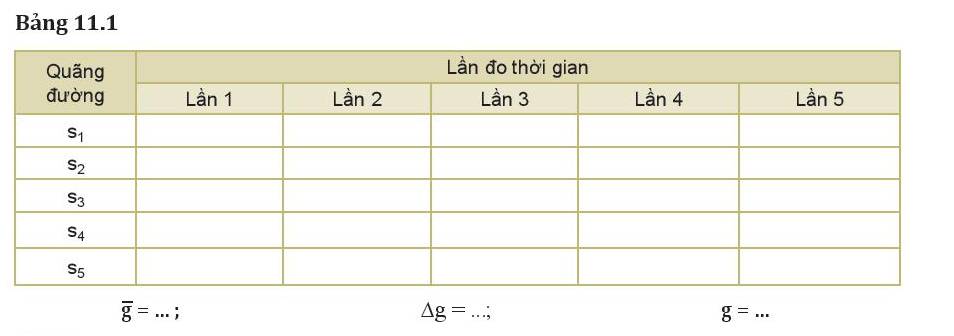
1. Tính giá trị trung bình và sai số tuyệt đối của phép đo gia tốc rơi tự do
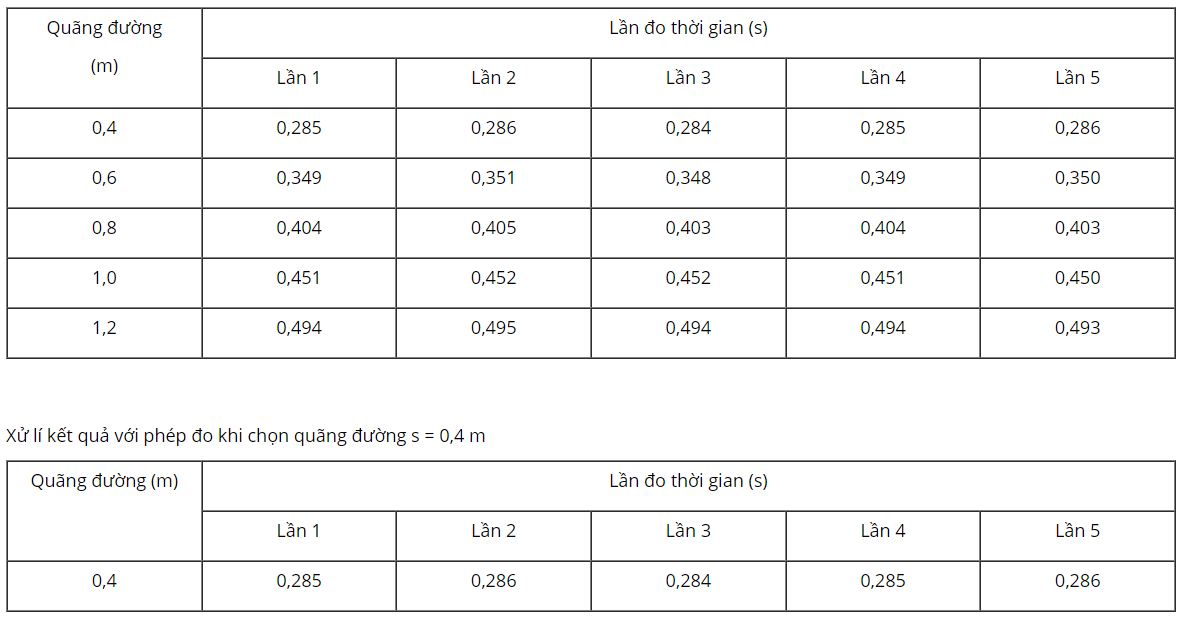
- Lần 1: \({g_1} = \frac{{2{s_1}}}{{t_1^2}} = \frac{{2.0,4}}{{0,{{285}^2}}} = 9,849(m/{s^2})\)
- Lần 2: \({g_2} = \frac{{2{s_2}}}{{t_2^2}} = \frac{{2.0,4}}{{0,{{285}^2}}} = 9,849(m/{s^2})\)
- Lần 3: \({g_3} = \frac{{2{s_3}}}{{t_3^2}} = \frac{{2.0,4}}{{0,{{285}^2}}} = 9,919(m/{s^2})\)
- Lần 4: \({g_4} = \frac{{2{s_4}}}{{t_4^2}} = \frac{{2.0,4}}{{0,{{285}^2}}} = 9,849(m/{s^2})\)
- Lần 5: \({g_5} = \frac{{2{s_5}}}{{t_5^2}} = \frac{{2.0,4}}{{0,{{286}^2}}} = 9,780(m/{s^2})\)
Gia tốc trung bình là: \(\overline g = \frac{{9,849 + 9,849 + 9,919 + 9,849 + 9,780}}{5} = 9,849(m/{s^2})\)
Sai số tuyệt đối của gia tốc trong các lần đo
\(\begin{array}{l}\Delta {g_1} = \left| {\overline g - {g_1}} \right| = \left| {9,849 - 9,849} \right| = 0\\\Delta {g_2} = \left| {\overline g - {g_2}} \right| = \left| {9,849 - 9,849} \right| = 0\\\Delta {g_3} = \left| {\overline g - {g_3}} \right| = \left| {9,849 - 9,919} \right| = 0,07\\\Delta {g_4} = \left| {\overline g - {g_4}} \right| = \left| {9,849 - 9,849} \right| = 0\\\Delta {g_5} = \left| {\overline g - {g_5}} \right| = \left| {9,849 - 9,780} \right| = 0,069\end{array}\)
Sai số tuyệt đối trung bình là: \(\overline {\Delta g} = \frac{{\Delta {g_1} + \Delta {g_2} + \Delta {g_3} + \Delta {g_4} + \Delta {g_5}}}{5} = 0,028\)
Suy ra kết quả: \(g = 9,849 \pm 0,028\)
2. Trong thí nghiệm người ta dùng trụ thép làm vật rơi nhằm mục đích khi ta thả vật rơi thì xác suất phương rơi của vật chắn tia hồng ngoại ở cổng quang điện cao, giúp ta thực hiện thí nghiệm dễ dàng hơn
- Có thể dùng vật thả rơi là viên bi thép, nhưng xác suất khi thả rơi viên bi có phương rơi không chắn được tia hồng ngoại cao hơn khi dùng trụ thép, nên khi làm thí nghiệm với viên bi ta cần căn chỉnh và thả theo đúng phương của dây rọi.

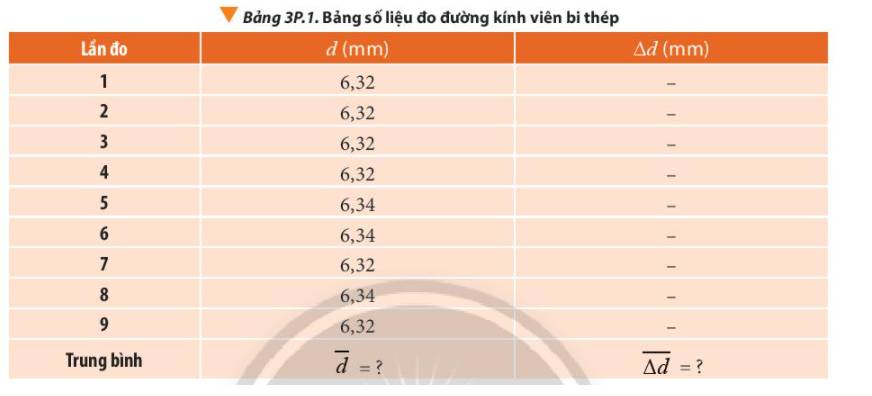
Giá trị trung bình của đường kính viên bi thép là:
\(\overline d = \frac{{{d_1} + {d_2} + ... + {d_9}}}{9} \approx 6,33(mm)\)
Sai số tuyệt đối ứng với mỗi lần đo là:
\(\begin{array}{l}\Delta {d_1} = \left| {\overline d - {d_1}} \right| = \left| {6,33 - 6,32} \right| = 0,01(mm) = \Delta {d_2} = \Delta {d_3} = \Delta {d_4} = \Delta {d_7} = \Delta {d_9}\\\Delta {d_5} = \left| {\overline d - {d_5}} \right| = \left| {6,33 - 6,34} \right| = 0,01(mm) = \Delta {d_6} = \Delta {d_8}\end{array}\)
Sai số tuyệt đối trung bình của phép đo:
\(\overline {\Delta d} = \frac{{\Delta {d_1} + \Delta {d_2} + ... + \Delta {d_9}}}{9} = 0,01(mm)\)
Sai số tuyệt đối của phép đo là:
\(\Delta d = \overline {\Delta d} + \Delta {d_{dc}} = 0,01 + 0,02 = 0,03(mm)\)



Các em thực hành theo hướng dẫn của giáo viên.
Ví dụ cho kết quả thí nghiệm
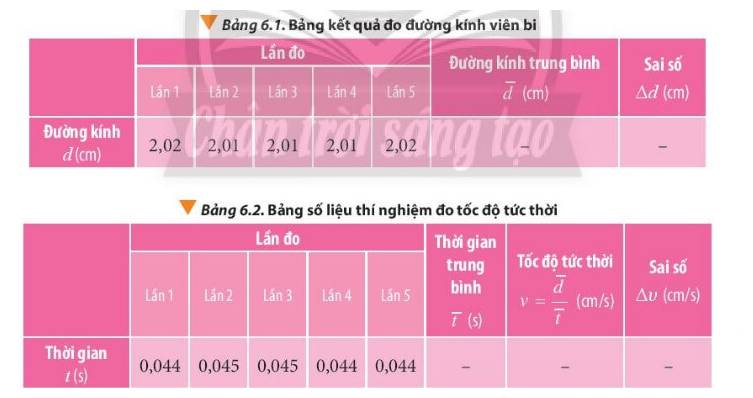
Bảng 6.1
Quãng đường: s = 0,5 (m)
- Tốc độ trung bình: \(\overline v = \frac{s}{{\overline t }} = \frac{{0,5}}{{0,778}} = 0,643(m/s)\)
- Sai số:
\(\begin{array}{l}\overline {\Delta t} = \frac{{\Delta {t_1} + \Delta {t_2} + ... + \Delta {t_n}}}{n} = \frac{{0,001 + 0,002 + 0,002}}{3} \approx 0,002(s)\\\delta t = \frac{{\overline {\Delta t} }}{{\overline t }}.100\% = \frac{{0,002}}{{0,778}}.100\% = 0,3\% \\\delta s = \frac{{\overline {\Delta s} }}{s}.100\% = \frac{{0,0005}}{{0,5}}.100\% = 0,1\% \\\delta v = \delta s + \delta t = 0,1\% + 0,3\% = 0,4\% \\\Delta v = \delta v.\overline v = 0,4\% .0,643 = 0,003\\ \Rightarrow v = 0,643 \pm 0,003(m/s)\end{array}\)
Bảng 6.2
Đường kính của viên bi: d = 0,02 (m); sai số: 0,02 mm = 0,00002 (m)
- Tốc độ tức thời: \(\overline v = \frac{d}{{\overline t }} = \frac{{0,02}}{{0,032}} = 0,625(m/s)\)
- Sai số:
\(\begin{array}{l}\overline {\Delta t} = \frac{{\Delta {t_1} + \Delta {t_2} + ... + \Delta {t_n}}}{n} = \frac{{0,001 + 0 + 0,00}}{3} \approx 0,001(s)\\\delta t = \frac{{\overline {\Delta t} }}{{\overline t }}.100\% = \frac{{0,001}}{{0,032}}.100\% = 2,1\% \\\delta s = \frac{{\overline {\Delta s} }}{s}.100\% = \frac{{0,00002}}{{0,02}}.100\% = 0,1\% \\\delta v = \delta s + \delta t = 0,1\% + 2,1\% = 2,2\% \\\Delta v = \delta v.\overline v = 2,2\% .0,0032 = 0,001\\ \Rightarrow v = 0,625 \pm 0,014(m/s)\end{array}\)
Nhận xét: Tốc độ trung bình gần bằng tốc độ tức thời, vì viên bi gần như chuyển động đều.