Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Có -a=b+c
<=> 0=a+b+c
Có \(\sqrt{\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}}=\sqrt{\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)^2-2\left(\frac{1}{ab}+\frac{1}{bc}+\frac{1}{ac}\right)}\)
=\(\sqrt{\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)^2-2.\frac{a+b+c}{abc}}\)
=\(\sqrt{\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)^2-2.\frac{0}{abc}}\)
=\(\sqrt{\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)^2}\)
= \(\left|\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right|\) là số hữu tỉ (vì a,b,c là số hữu tỉ)
=> \(\sqrt{\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}}\) là số hữu tỉ

\(\frac{1}{x^2}+\frac{1}{y^2}+\frac{1}{z^2}=\frac{\left(xy+yz+zx\right)^2}{x^2y^2z^2}\)(1) với x+y+z=0. Bạn quy đồng vế trái (1) dc \(\frac{x^2y^2+y^2z^2+z^2x^2}{x^2y^2z^2}=\frac{\left(xy+yz+zx\right)^2-2\left(x+y+z\right)xyz}{x^2y^2z^2}\)

\(f\left(1+\sqrt{2}\right)=2019\Rightarrow a\left(1+\sqrt{2}\right)^2+b\left(1+\sqrt{2}\right)+2018=2019\)
\(\Leftrightarrow a\left(3+2\sqrt{2}\right)+b\left(1+\sqrt{2}\right)=1\)
\(\Leftrightarrow3a+2a\sqrt{2}+b+b\sqrt{2}=1\)
\(\Leftrightarrow\left(2a+b\right)\sqrt{2}=1-3a-b\)
Do vế phải là số hữu tỉ nên vế trái hữu tỉ, mà \(\sqrt{2}\) vô tỉ nên vế phải hữu tỉ khi và chỉ khi \(2a+b=0\)
\(\Rightarrow\left\{{}\begin{matrix}2a+b=0\\1-3a-b=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}2a+b=0\\3a+b=1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=1\\b=-2\end{matrix}\right.\)

zZz Cậu bé Zỗi hơi zZz
Số học sinh trường A và trường B :
420 : 84% = 500 học sinh
Gọi x ; y lần lượt là trường A và B
= > x + y = 500 ﴾1﴿
Số học sinh đỗ trường A là :
80% x = 0,8 x ﴾học sinh﴿
Số học sinh đỗ trường B là :
90% y = 0,9 y ﴾học sinh ﴿
Ta có: Tổng số học sinh trung bình khối 8 và 9 là: 0,8x + 0,9 y = 420 ﴾2﴿
0.8x + 0.9y = 352.8
=> x = 252 và y = 168

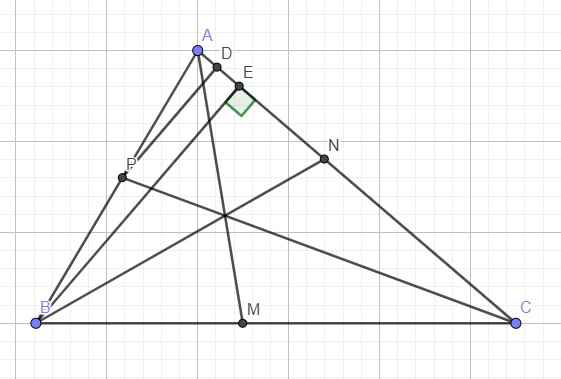
Kẻ PD và BE vuông góc AC
Định lý phân giác: \(\dfrac{AN}{NC}=\dfrac{AB}{BC}\Rightarrow\dfrac{AN}{AN+NC}=\dfrac{AB}{AB+BC}\Rightarrow\dfrac{AN}{AC}=\dfrac{AB}{AB+BC}=\dfrac{c}{a+c}\)
Tương tự: \(\dfrac{AP}{AB}=\dfrac{b}{a+b}\)
Talet: \(\dfrac{PD}{BE}=\dfrac{AP}{AB}\)
\(\dfrac{S_{APN}}{S_{ABC}}=\dfrac{\dfrac{1}{2}PD.AN}{\dfrac{1}{2}BE.AC}=\dfrac{AP}{AB}.\dfrac{AN}{AC}=\dfrac{bc}{\left(a+b\right)\left(a+c\right)}\)
Tương tự: \(\dfrac{S_{BPM}}{S_{ABC}}=\dfrac{ac}{\left(a+b\right)\left(b+c\right)}\) ; \(\dfrac{S_{CMN}}{S_{ABC}}=\dfrac{ab}{\left(a+c\right)\left(b+c\right)}\)
\(\Rightarrow\dfrac{S_{APN}+S_{BPM}+S_{CMN}}{S_{ABC}}=\dfrac{bc}{\left(a+b\right)\left(a+c\right)}+\dfrac{ac}{\left(a+b\right)\left(b+c\right)}+\dfrac{ab}{\left(a+c\right)\left(b+c\right)}\)
\(\Rightarrow\dfrac{S_{MNP}}{S_{ABC}}=\dfrac{S_{ABC}-\left(S_{APN}+S_{BPM}+S_{CMN}\right)}{S_{ABC}}=1-\left(\dfrac{bc}{\left(a+b\right)\left(a+c\right)}+\dfrac{ac}{\left(a+b\right)\left(b+c\right)}+\dfrac{ab}{\left(a+c\right)\left(b+c\right)}\right)\)
\(=\dfrac{2abc}{\left(a+b\right)\left(b+c\right)\left(c+a\right)}\)
2. Do ABC cân tại C \(\Rightarrow AC=BC=a\)
\(\dfrac{BC}{AB}=k\Rightarrow AB=\dfrac{BC}{k}=\dfrac{a}{k}\)
Do đó:
\(\dfrac{S_{MNP}}{S_{ABC}}=\dfrac{2abc}{\left(a+b\right)\left(b+c\right)\left(c+a\right)}=\dfrac{2.a.a.\dfrac{a}{k}}{2a.\left(a+\dfrac{a}{k}\right)\left(a+\dfrac{a}{k}\right)}=\dfrac{k}{\left(k+1\right)^2}\)
Cho 3 **** kiểu gì nào?
a) a,b có thể là số vô tỉ. Ví dụ \(a=b=\sqrt{2}\) là vô tỉ mà ab và a/b đều hữu tỉ.
b) Trong trường hợp này \(a,b\) không là số vô tỉ (tức cả a,b đều là số hữu tỉ). Thực vậy theo giả thiết \(a=bt\), với \(t\) là số hữu tỉ khác \(-1\). Khi đó \(a+b=b\left(1+t\right)=s\) là số hữu tỉ, suy ra \(b=\frac{s}{1+t}\) là số hữu tỉ. Vì vậy \(a=bt\) cũng hữu tỉ.
c) Trong trường hợp này \(a,b\) có thể kaf số vô tỉ. Ví dụ ta lấy \(a=1-\sqrt{3},b=3+\sqrt{3}\to a,b\) vô tỉ nhưng \(a+b=4\) là số hữu tỉ và \(a^2b^2=\left(ab\right)^2=12\) cũng là số hữu tỉ.