Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi x là số sản phẩm sản xuất trong một ngày theo định mức.
Điều kiện x nguyên dương. Theo đề ta có chương trình:
\(\dfrac{360}{x}=\dfrac{360+\dfrac{360.5}{100}}{x+9}+1\)
⇔ x2 + 27x – 3240 = 0
⇒ x1= -72 (loại), x2 = 45.
Thời gian giao hoàn thành kế hoạch là = 8 ngày
Nếu sản xuất theo thời gian đã định với năng suất mới thì số sản phẩm làm được là (45+9).8=432 sản phẩm.

Gọi x (ngày) là số ngày dự định làm xong kế hoạch (x > 0).
Khi đó:
Số sản phẩm dự định làm trong một ngày là: 360/x (sản phẩm)
Thực tế, mỗi ngày làm thêm được 9 sản phẩm nên năng suất thực tế là: 360/x + 9 (sản phẩm / ngày)
Số ngày làm thực tế là: x – 1 (ngày)
Số sản phẩm làm được trong x – 1 ngày là: 360 + 360.5% = 378 sản phẩm.
Ta có phương trình:
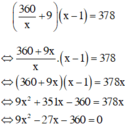
⇔ x = 8 (thỏa mãn) hoặc x = –5 (loại)
Số ngày dự định là 8 ngày, năng suất thực tế là 360:8 + 9 = 54 sản phẩm/ngày
Vậy khi đến hạn, phân xưởng sẽ làm được 54.8 = 432 sản phẩm.

\(\Leftrightarrow\left(x-y+m\right)^2+y^2+2\left(m+1\right)y-m^2+25\ge0\); \(\forall x;y\)
\(\Leftrightarrow y^2+2\left(m+1\right)y-m^2+25\ge0\) ;\(\forall y\)
\(\Leftrightarrow\Delta'=\left(m+1\right)^2-\left(-m^2+25\right)\le0\)
\(\Leftrightarrow m^2+m-12\le0\Rightarrow-4\le m\le3\)

Điều kiện xác định: x ≠ 0 .
Đặt t = x + 1 x ⇒ t 2 − 2 = x 2 + 1 x 2 ≥ 2 ⇒ t ≥ 2 ⇔ t ≥ 2 t ≤ − 2
Phương trình đã cho trở thành 2 t 2 − 2 − 3 t − 2 m + 1 = 0
⇔ 2 t 2 − 3 t − 2 m − 3 = 0 ⇔ 2 t 2 − 3 t − 3 = 2 m ( 1 )
Xét hàm số y = f ( t ) = 2 t 2 − 3 t − 3 có bảng biến thiên:

(1) Có nghiệm t thỏa mãn
t
≥
2
t
≤
−
2
k
h
i
2
m
≥
−
1
2
m
≥
11
⇔
m
≥
−
1
2
⇒
S
=
−
1
2
;
+
∞
Vậy T = 3
Đáp án cần chọn là: D

Đặt x + 1 t = t , t ≥ 2 khi đó phương trình trở thành 2 t 2 − 3 t − 5 m − 3 = 0 ( * )
Phương trình 2 x 2 + 1 x 2 - 3 x + 1 x - 5 m + 1 = 0 có nghiệm khi và chỉ khi phương trình (*) có nghiệm t thỏa mãn t ≥ 2
Số nghiệm của phương trình (*) bằng số giao điểm của parabol (P): y = 2 t 2 − 3 t − 3 và đường thẳng d : y = 5 m
Xét parabol P : y = 2 t 2 - 3 t - 3 ta có bảng biến thiên như sau:
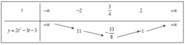
Từ bảng biến thiên ta có phương trình (*) có nghiệm t ∈ ( - ∞ ; - 2 ] ∪ [ 2 ; + ∞ ) khi và chỉ khi 5 m ≥ - 1 hoặc 5 m ≥ 11
![]()
Vậy khi m ∈ − 1 5 ; + ∞ thì phương trình có nghiệm ⇒ a = 1 b = 5 ⇒ T = 5
Đáp án cần chọn là: B

Ví dụ, ta có bảng đo chiều cao của các bạn trong tổ như sau:
160 | 162 | 164 | 165 | 172 | 174 | 177 | 178 | 180 |
a) Sắp xếp mẫu số liệu theo thứ tự không giảm ta được:
160 162 164 165 172 174 177 178 180
Số trung bình cộng của mẫu số liệu trên là:
\(\overline x = \frac{{160\;\; + 162\;\; + 164\;\;\; + \;\;165\;\; + \;172\;\; + \;174\;\; + \;177\; + \;\;178\; + \;180}}{9} = \frac{{1532}}{9}\)
Trung vị của mẫu số liệu trên là: Do mẫu số liệu trên có 9 số liệu ( lẻ ) nên trung vị \({Q_2} = 172\)
Tứ phân vị của mẫu số liệu trên là:
- Trung vị của dãy 160 162 164 165 là: \({Q_1} = 163\)
- Trung vị của dãy 174 177 178 180 là: \({Q_3} = 177,5\)
- Vậy tứ phân vị của mẫu số liệu là: \({Q_1} = 163\), \({Q_2} = 172\), \({Q_3} = 177,5\)
b) Khoảng biến thiên của mẫu số liệu trên là: \(R = {x_{\max }} - {x_{\min }} = 180 - 160 = 20\)
Khoảng tứ phân vị của mẫu số liệu trên là: \({\Delta _Q} = {Q_3} - {Q_1} = 177,5 - 163 = 14,5\)
c) Phương sai của mẫu số liệu trên là:
\({s^2} = \frac{{\left[ {{{\left( {160 - \overline x } \right)}^2} + {{\left( {162 - \overline x } \right)}^2} + ... + {{\left( {180 - \overline x } \right)}^2}} \right]}}{9} \approx 50,84\)
Độ lệch chuẩn của mẫu số liệu trên là: \(s = \sqrt {{s^2}} \approx 7,13\)