Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Với bất kì \({x_0} \in \mathbb{R}\), ta có:
\(f'\left( {{x_0}} \right) = \mathop {\lim }\limits_{x \to {x_0}} \frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}} = \mathop {\lim }\limits_{x \to {x_0}} \frac{{x - {x_0}}}{{x - {x_0}}} = \mathop {\lim }\limits_{x \to {x_0}} 1 = 1\)
Vậy \(f'\left( x \right) = {\left( x \right)^\prime } = 1\) trên \(\mathbb{R}\).
b) Ta có:
\(\begin{array}{l}{\left( {{x^2}} \right)^\prime } = 2{\rm{x}}\\{\left( {{x^3}} \right)^\prime } = 3{{\rm{x}}^2}\\...\\{\left( {{x^n}} \right)^\prime } = n{{\rm{x}}^{n - 1}}\end{array}\)

a) Đồ thị hàm số (hình bên).
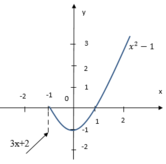
Quan sát đồ thị nhận thấy :
+ f(x) liên tục trên các khoảng (-∞ ; -1) và (-1 ; ∞).
+ f(x) không liên tục tại x = -1.
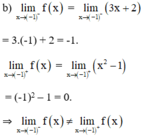
⇒ không tồn tại giới hạn của f(x) tại x = -1.
⇒ Hàm số không liên tục tại x = -1.

a) • \(y = f\left( x \right) = \frac{1}{{x - 1}}\)
ĐKXĐ: \(x - 1 \ne 0 \Leftrightarrow x \ne 1\)
Vậy hàm số có tập xác định: \(D = \mathbb{R}\backslash \left\{ 1 \right\}\).
• \(y = g\left( x \right) = \sqrt {4 - x} \)
ĐKXĐ: \(4 - x \ge 0 \Leftrightarrow x \le 4\)
Vậy hàm số có tập xác định: \(D = \left( { - \infty ;4} \right]\).
b) • Với mọi \({x_0} \in \left( { - \infty ;1} \right)\), ta có:
\(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = \mathop {\lim }\limits_{x \to {x_0}} \frac{1}{{x - 1}} = \frac{{\mathop {\lim }\limits_{x \to {x_0}} 1}}{{\mathop {\lim }\limits_{x \to {x_0}} x - \mathop {\lim }\limits_{x \to {x_0}} 1}} = \frac{1}{{{x_0} - 1}} = f\left( {{x_0}} \right)\)
Vậy hàm số \(y = f\left( x \right)\) liên tục tại mọi điểm \({x_0} \in \left( { - \infty ;1} \right)\).
Tương tự ta có hàm số \(y = f\left( x \right)\) liên tục tại mọi điểm \({x_0} \in \left( {1; + \infty } \right)\).
Ta có: Hàm số không xác định tại điểm \({x_0} = 1\)
\(\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ + }} \frac{1}{{x - 1}} = + \infty ;\mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ - }} \frac{1}{{x - 1}} = - \infty \)
Vì \(\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) \ne \mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right)\) nên không tồn tại \(\mathop {\lim }\limits_{x \to 1} f\left( x \right)\).
Vậy hàm số \(y = f\left( x \right)\) không liên tục tại điểm \({x_0} = 1\).
• Với mọi \({x_0} \in \left( { - \infty ;4} \right)\), ta có:
\(\mathop {\lim }\limits_{x \to {x_0}} g\left( x \right) = \mathop {\lim }\limits_{x \to {x_0}} \sqrt {4 - x} = \sqrt {\mathop {\lim }\limits_{x \to {x_0}} 4 - \mathop {\lim }\limits_{x \to {x_0}} x} = \sqrt {4 - {x_0}} = g\left( {{x_0}} \right)\)
Vậy hàm số \(y = g\left( x \right)\) liên tục tại mọi điểm \({x_0} \in \left( { - \infty ;4} \right)\).
Ta có: \(g\left( 4 \right) = \sqrt {4 - 4} = 0\)
\(\mathop {\lim }\limits_{x \to {4^ - }} g\left( x \right) = \mathop {\lim }\limits_{x \to {4^ - }} \sqrt {4 - x} = \sqrt {\mathop {\lim }\limits_{x \to {4^ - }} 4 - \mathop {\lim }\limits_{x \to {4^ - }} x} = \sqrt {4 - 4} = 0 = g\left( 4 \right)\)
Vậy hàm số \(y = g\left( x \right)\) liên tục tại điểm \({x_0} = 4\).
Hàm số không xác định tại mọi \({x_0} \in \left( {4; + \infty } \right)\) nên hàm số \(y = g\left( x \right)\) không liên tục tại mọi điểm \({x_0} \in \left( {4; + \infty } \right)\).
Vậy hàm số \(y = g\left( x \right)\) liên tục trên nửa khoảng \(\left( { - \infty ;4} \right]\).

a) Hàm hằng ⇒ Δy = 0
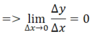
b) theo định lí 1
y = x hay y = x1 ⇒ y’= (x1)’= 1. x1-1 = 1. xo = 1.1 =1
a: Nếu a là số nguyên dương thì TXĐ là D=R
Nếu a là số không phải nguyên dương thì TXĐ là D=R\{0}
Nếu a không là số nguyên thì TXĐ: D=R
b: \(y'=\left(x^a\right)'=\left(e^{a\cdot lnx}\right)'\)
\(=\dfrac{a}{x}\cdot e^{a\cdot lnx}=\dfrac{a}{x}\cdot x^a=a\cdot x^{a-1}\)