Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a, Ta có : \(\dfrac{98x^2-2}{x-2}=0\Leftrightarrow\left\{{}\begin{matrix}98x^2-2=0\\x-2\ne0\end{matrix}\right.\)
hay \(\left\{{}\begin{matrix}x^2=\dfrac{1}{49}\\x\ne2\end{matrix}\right.\Leftrightarrow x=\pm\dfrac{1}{7}\)
Vậy giá trị của phân thức này bằng 0 khi \(x=\pm\dfrac{1}{7}\)
b, Ta có : \(\dfrac{3x-2}{x^2+2x+1}=0\Leftrightarrow\dfrac{3x-2}{\left(x+1\right)^2}=0\Leftrightarrow\left\{{}\begin{matrix}3x-2=0\\\left(x+1\right)^2\ne0\end{matrix}\right.\)
hay \(\left\{{}\begin{matrix}x=\dfrac{2}{3}\\x\ne-1\end{matrix}\right.\)
Vậy giá trị của phân thức này bằng 0 khi \(x=\dfrac{2}{3}\)
a)
98x^2 -2 =0 =>x^2 =1/49 => x= -+1/7 nhận
b)
3x-2=0=>x=2/3 nhận
Thay \(x = - 2\); \(y = \dfrac{1}{3}\) vào đa thức \(A\) ta có:
\(\begin{array}{l}A = 5.{\left( { - 2} \right)^2} - 4.\left( { - 2} \right).\dfrac{1}{3} + 2.\left( { - 2} \right) - 4.{\left( { - 2} \right)^2} + \left( { - 2} \right).\dfrac{1}{3}\\A = 5.4 - \dfrac{{ - 8}}{3} + \left( { - 4} \right) - 4.4 + \dfrac{{ - 2}}{3}\\A = 20 + \dfrac{8}{3} - 4 - 16 + \dfrac{{ - 2}}{3}\\A = 2\end{array}\)
Thay \(x = - 2\); \(y = \dfrac{1}{3}\) vào đa thức \(B\) ta có:
\(\begin{array}{l}B = {\left( { - 2} \right)^2} - 3.\left( { - 2} \right).\dfrac{1}{3} + 2.\left( { - 2} \right)\\B = 4 - \left( { - 2} \right) + \left( { - 4} \right)\\B = 4 + 2 - 4\\B = 2\end{array}\)
Vậy \(A = B\)
bài 1:
a, x^2-2x = x*(x-2)
b, x^2 -xy+x-y = x*(x-y) + (x-y)
= (x-y) (x+1)
B) Ta có: 2x-2y-x2+2xy-y2
⇔ 2(x-y)-(x2-2xy+y2)
⇔ 2(x-y)-(x-y)2
⇔ (x-y)(2-x+y)
Đúng thì tick nhé
Phân thức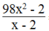 
= 0 khi
98
x
2
+
2
=
0
và x – 2
≠
0
Ta có: x – 2 ≠ 0 ⇔ x ≠ 2
98 x 2 + 2 = 0 ⇔ 2 49 x 2 - 1 = 0 ⇔ (7x + 1)(7x – 1) = 0
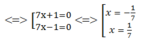
Ta có: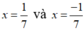 
thỏa mãn điều kiện x
≠
2
Vậy 
thì phân thức 
có giá trị bằng 0.
Phân thức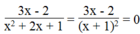 
khi 3x – 2 = 0 và
x
+
1
2
≠
0
Ta có: x + 1 2 ≠ 0 ⇔ x + 1 ≠ 0 ⇔ x ≠ - 1
3x – 2 = 0 ⇔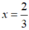 
Ta có: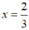 
thỏa mãn điều kiện x
≠
- 1
Vậy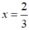 
thì phân thức 
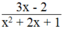có giá trị bằng 0.
bbgfhfygfdsdty64562gdfhgvfhgfhhhhh
\hvhhhggybhbghhguyg
a, \(M=\frac{xy^2+y^2\left(y^2-x\right)+1}{x^2y^4+2y^4+x^2+2}=\frac{y^2\left(x+y^2-x\right)+1}{y^4\left(x^2+2\right)+\left(x^2+2\right)}=\frac{y^4+1}{\left(y^4+1\right)\left(x^2+2\right)}=\frac{1}{x^2+2}\)
Thay x=-3 vào M
=>\(M=\frac{1}{\left(-3\right)^2+2}=\frac{1}{11}\)
b, Vì \(x^2\ge0\Rightarrow x^2+2\ge2\Rightarrow M=\frac{1}{x^2+2}>0\)
a) Điều kiện xác định của phân thức \(M\): \(y \ne 0\)
Điều kiện xác định của phân thức \(N\): \(xy + y \ne 0\) hay \(xy \ne - y\)
Khi \(x = 3\), \(y = 2\) (thoả mãn điều kiện xác định), ta có:
\(M = \dfrac{3}{2}\)
\(N = \dfrac{{{3^2} + 3}}{{3.2 + 2}} = \dfrac{{9 + 3}}{{6 + 2}} = \dfrac{{12}}{8} = \dfrac{3}{2}\)
Vậy \(M = N = \dfrac{3}{2}\) khi \(x = 3\), \(y = 2\)
Khi \(x = - 1\), \(y = 5\) (thỏa mãn điều kiện xác định của \(M\)) ta có:
\(M = \dfrac{{ - 1}}{5}\)
Vậy \(M = \dfrac{{ - 1}}{5}\) khi \(x = - 1\), \(y = 5\)
Khi \(x = - 1\), \(y = 5\) thì \(xy + y = \left( { - 1} \right).5 + 5 = 0\) nên không thỏa mãn điều kiện xác định của \(N\). Vậy giá trị của phân thức \(N\) tại \(x = - 1\), \(y = 5\) không xác định.
b) Ta có:
\(x.\left( {xy + y} \right) = {x^2}y + xy\)
\(\left( {{x^2} + x} \right).y = {x^2}y + xy\)
Vậy \(x\left( {xy + y} \right) = \left( {{x^2} + x} \right)y\)