Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Vẽ lại hình.
b) Ghi số đo ứng với các góc còn lại ta được hình bên:
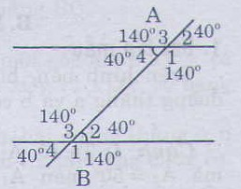
c) Ta có:
góc A4 + A1 = 180độ
=> góc A1 = 180 độ - 40 độ = 140 độ
=> góc A1 + góc B2= 40độ + 140 độ = 180 độ
Ý 2
Ta có:
góc B3 + góc B2 = 180 độ
=> góc B3 = 180 độ - 40 độ = 140 độ
=> góc A4 + B3 = 140 độ + 40 độ = 180 độ

a, Vì góc A1 = góc A3 (đối đỉnh) => góc A1 = góc A3 = 90 độ
Mà góc A3 + góc A4 = 180 độ (kề bù)
=> góc A4 = 180 độ - A3 = 180 độ - 90 độ = 90 độ
b, Ta có:
góc A1 - góc A2 = 100 độ
+
góc A1 + góc A2 = 180 độ
_______________________
2A1 = 280 độ
=> góc A1 = 280 độ : 2 = 140 độ
=> góc A3 = góc A1 = 140 độ (đối điỉnh)
Mà góc A3 + góc A4 = 180 độ (kề bù)
=> góc A4 = 180 độ - góc A3 = 180 độ - 140 độ = 40 độ
c, 2A1 = A4 => 2A3 = A4 (do A1 = A3 (đối đỉnh))
Ta có: A3 + A4 = 180 độ (kề bù)
=> A3 + 2A3 = 180 độ
=> 3A3 = 180 độ
=> A3 = 60 độ
=> A4 = 120 độ
a, Vì góc A1 = góc A3 (đối đỉnh) => góc A1 = góc A3 = 90 độ
Mà góc A3 + góc A4 = 180 độ (kề bù)
=> góc A4 = 180 độ - A3 = 180 độ - 90 độ = 90 độ
b, Ta có:
góc A1 - góc A2 = 100 độ
+
góc A1 + góc A2 = 180 độ
_______________________
2A1 = 280 độ
=> góc A1 = 280 độ : 2 = 140 độ
=> góc A3 = góc A1 = 140 độ (đối điỉnh)
Mà góc A3 + góc A4 = 180 độ (kề bù)
=> góc A4 = 180 độ - góc A3 = 180 độ - 140 độ = 40 độ
c, 2A1 = A4 => 2A3 = A4 (do A1 = A3 (đối đỉnh))
Ta có: A3 + A4 = 180 độ (kề bù)
=> A3 + 2A3 = 180 độ
=> 3A3 = 180 độ
=> A3 = 60 độ
=> A4 = 120 độ

a22=a1 . a2 ; a32=a2 . a4
=> \(\frac{a_1}{a_2}=\frac{a_2}{a_3};\frac{a_2}{a_3}=\frac{a_3}{a_4}\)
=> \(\frac{a_1}{a_2}=\frac{a_2}{a_3}=\frac{a_3}{a_4}\)= \(\frac{a_1+a_2+a_3}{a_2+a_3+a_4}\)
=> \(\frac{a1^3+a2^3+a3^3}{a2^3+a3^3+a4^3}=\frac{a1.a2.a3}{a2.a3.a4}=\frac{a1}{a4}\)

Theo đề bài \(a_2^2=a_1a_3\) và \(a_3^2=a_2a_4\) do đó \(\frac{a_1}{a_2}=\frac{a_2}{a_3}\) và \(\frac{a_2}{a_3}=\frac{a_3}{a_4}\)
hay \(\frac{a_1}{a_2}=\frac{a_2}{a_3}=\frac{a_3}{a_4}\), suy ra \(\frac{a_1^3}{a_2^3}=\frac{a_2^3}{a_3^3}=\frac{a_3^3}{a_4^3}=\frac{a_1}{a_2}\cdot\frac{a_2}{a_3}\cdot\frac{a_3}{a_4}=\frac{a_1}{a_4}\left(1\right)\)
Mặt khác \(\frac{a_1^3}{a_2^3}=\frac{a_2^3}{a_3^3}=\frac{a_3^3}{a_4^3}=\frac{a_1^3+a_2^3+a_3^3}{a_2^3+a_3^3+a_4^3}\left(2\right)\)
Từ (1) và (2) ta có điều phải chứng minh

Áp dụng tính chất của dãy tỉ số = nhau ta có:
\(\frac{a_1}{a_2}=\frac{a_2}{a_3}=\frac{a_3}{a_4}=\frac{a_1+a_2+a_3}{a_2+a_3+a_4}\)
=> \(\frac{a_1}{a_2}.\frac{a_2}{a_3}.\frac{a_3}{a_4}=\left(\frac{a_1+a_2+a_3}{a_2+a_3+a_4}\right)^3\)
=> \(\frac{a_1}{a_4}=\left(\frac{a_1+a_2+a_3}{a_2+a_3+a_4}\right)^3\left(đpcm\right)\)


