Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

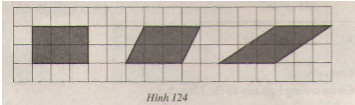
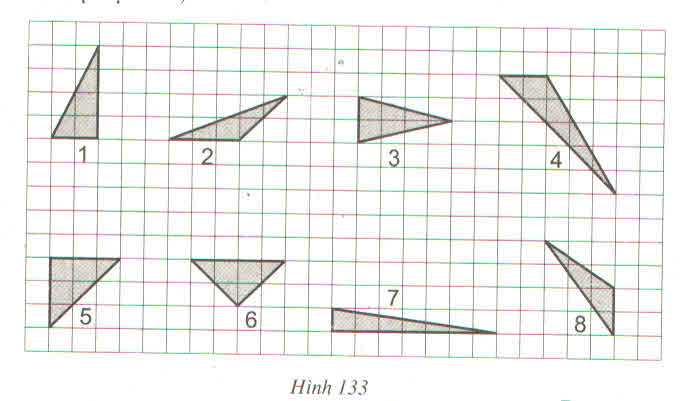
a) Các tam giác số 1, 3, 6 có cùng diện tích là 4 ô vuông.
Các tam giác số 2, 8 có cùng diện tích là 3 ô vuông.
Các tam giác số 4, 5, 7 không có cùng diện tích với các tam giác nào khác(diện tích tam giác số 4 là 5 ô vuông, tam giác số là 4,5 ô vuông, tam giác số 7 là 3,5 ô vuông).
b) Hai tam giác có diện tích bằng nhau thì chưa chắc hai tam giác đó đã bằng nhau.
a) Các tam giác số 1, 3, 6 có cùng diện tích là 4 ô vuông.
Các tam giác số 2, 8 có cùng diện tích là 3 ô vuông.
Các tam giác số 4, 5, 7 không có cùng diện tích với các tam giác nào khác(diện tích tam giác số 4 là 5 ô vuông, tam giác số là 4,5 ô vuông, tam giác số 7 là 3,5 ô vuông).
b) Hai tam giác có diện tích bằng nhau thì chưa chắc hai tam giác đó đã bằng nhau.

Diện tích hình a là 6 ô vuông
Diện tích hình b ∆ADH = ∆ BCI nên diện tích hình b sẽ bằng diện tích hình a (ABIH).
Vậy diện tích hình b là 6 ô vuông
Diện tích hình c: ∆ KLN = ∆ NMO nên diện tích hình c sẽ bằng diện tích hình a (KMCB).
Vậy diện tích hình c là 6 ô vuông
Diện tích hình a là 6 ô vuông
Diện tích hình b ∆ADH = ∆ BCI nên diện tích hình b sẽ bằng diện tích hình a (ABIH).
Vậy diện tích hình b là 6 ô vuông
Diện tích hình c: ∆ KLN = ∆ NMO nên diện tích hình c sẽ bằng diện tích hình a (KMCB).
Vậy diện tích hình c là 6 ô vuông

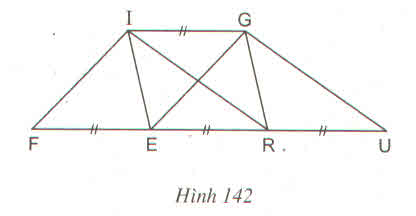
Ta có IG // FU nên khoảng cách giữa hai đường thẳng IG và FU không đổi và bằng h. Các hình bình hành FIGE, IGRE, IGUR có cạnh bằng nhau FE = ER = RU có cùng chiều cao ứng với cạnh đó nên diện tích chúng bằng nhau. Tức là SFIGR = SIGRE = SIGUR( = h. FE)
Mặt khác các tam giác IFG, GEU có cạnh đáy FR và EU bằng nhau, bằng hai lần cạnh hình bình hành FIGE nên diện tích chúng bằng nhau:
SIFR = SGEU = SFIGE
Vậy SFIGE = SIGRE = SIGUR = SIFR = SGEU
Ta có IG // FU nên khoảng cách giữa hai đường thẳng IG và FU không đổi và bằng h. Các hình bình hành FIGE, IGRE, IGUR có cạnh bằng nhau FE = ER = RU có cùng chiều cao ứng với cạnh đó nên diện tích chúng bằng nhau. Tức là SFIGR = SIGRE = SIGUR( = h. FE)
Mặt khác các tam giác IFG, GEU có cạnh đáy FR và EU bằng nhau, bằng hai lần cạnh hình bình hành FIGE nên diện tích chúng bằng nhau:
SIFR = SGEU = SFIGE
Vậy SFIGE = SIGRE = SIGUR = SIFR = SGEU

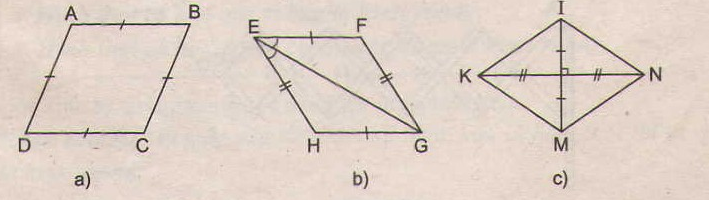
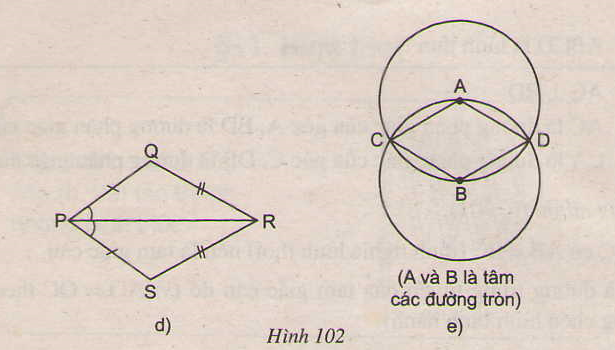
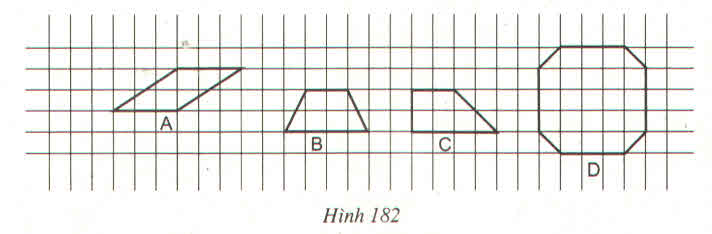
73. Tìm các hình thoi trên hình 102.
Bài giải:
Các tứ giác ở hình 39 a, b, c, e là hình thoi.
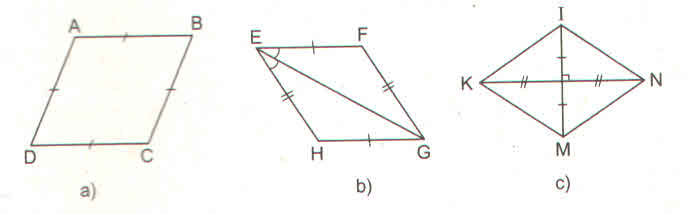
- Ở hình 102a, ABCD là hình thoi (theo định nghĩa)
- Ở hình 102b, EFGH là hình thoi (theo dấu hiệu nhận biết 4)
- Ở hình 102c, KINM là hình thoi (theo dấu hiệu nhận biết 3)
-Ở hình 102e, ADBC là hình thoi (theo định nghĩa, vì AC = AD = AB = BD = BC)
Tứ giác trên hình 102d không là hình thoi.
Các tứ giác ở hình 39 a, b, c, e là hình thoi.
- Ở hình 102a, ABCD là hình thoi (theo định nghĩa)
- Ở hình 102b, EFGH là hình thoi (theo dấu hiệu nhận biết 4)
- Ở hình 102c, KINM là hình thoi (theo dấu hiệu nhận biết 3)
-Ở hình 102e, ADBC là hình thoi (theo định nghĩa, vì AC = AD = AB = BD = BC)
Tứ giác trên hình 102d không là hình thoi.

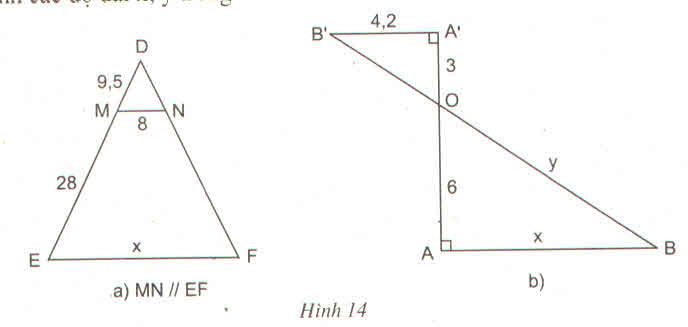
* Trong hình 14a
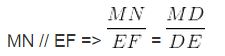
mà DE = MD + ME = 9.5 + 28 = 37.5

* Trong hình 14b
Ta có A’B’ ⊥ AA'(gt) và AB ⊥ AA'(gt)
=> A’B’ // AB =>


∆ABO vuông tại A
=> OB2 = y2 = OA2 + AB2
=> y2 = 62+ 8,42
=> y2 = 106,56
=> y ≈ 10,3

A B C D E F H G L M N P
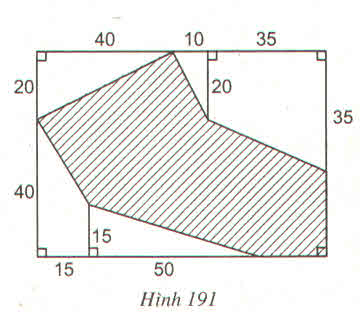
Độ dài chiều rộng của hình chữ nhật ABCD là:
20 + 40 = 60 (m)
Độ dài chiều dài của hình chữ nhật ABCD là:
40 + 10 + 35 = 85 (m)
Diện tích hình chữ nhật ABCD là:
60 . 85 = 5100 (m2).
Diện tích tam giác vuông HEN là:
\(\dfrac{10.20}{2}\)= \(\dfrac{200}{2}=100\left(m^2\right)\)
Diện tích tam giác vuông AHG là:
\(\dfrac{20.40}{2}=\dfrac{800}{2}=400\left(m^2\right)\)
Diện tích tam giác vuông MLP là:
\(\dfrac{15.50}{2}=\dfrac{750}{2}=375\left(m^2\right)\)
Diện tích hình thang vuông EBNF là:
\(\dfrac{\left(20+35\right).35}{2}=\dfrac{1925}{2}=962,5\left(m^2\right)\)
Diện tích hình thang vuông GMCL là:
\(\dfrac{\left(40+15\right).15}{2}=\dfrac{825}{2}=412,5\left(m^2\right)\)
Tổng diện tích các hình nằm ngoài hình gạch sọc và nằm trong hình chữ nhật ABCD là:
100 + 400 + 375 + 962,5 + 412,5 = 2250 (m2).
Diện tích hình sọc dọc là:
5100 - 2250 = 2850 (m2).
Vậy diện tích hình sọc dọc là 2850m2.

Ta có:
SABCD=(40+10+35).(20+40) = 5100 (cm2)
S1=\(\dfrac{40.20}{2}=400\left(cm^2\right)\)
S2=\(\dfrac{10.20}{2}=100\left(cm^2\right)\)
S3=\(\dfrac{\left(20+35\right).35}{2}=962,5\left(cm^2\right)\)
S4=\(\dfrac{50.15}{2}=375\left(cm^2\right)\)
S5=\(\dfrac{\left(15+40\right).15}{2}=412,5\left(cm^2\right)\)
=> Shình gạch sọc= S - ( S1+S2+S3+S4+S5)= 5100-(400+100+962,5+375+412,5)=2850(cm2)
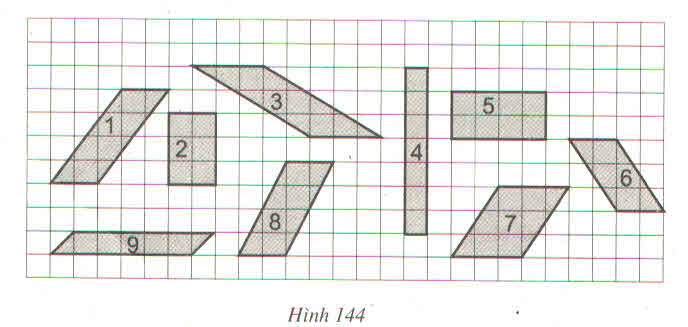





Các hình 2,6,9 có cùng diện tích là 6 ô vuông.
Các hình 1, 5, 8 có cùng diện tích là 8 ô vuông.
Các hình 3,7 có cùng diện tích là 8 ô vuông.
Hình 4 có diện tích là 7 ô vuông nên không có diện tích với một trong các hình đã cho.
Các hình 2, 6, 9 có cùng diện tích là 6 ô vuông.
Các hình 1, 5, 8 có cùng diện tích là 8 ô vuông.
Các hình 3, 7 có cùng diện tích là 9 ô vuông.