K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
KS
0
CH
Cô Hoàng Huyền
Admin
VIP
20 tháng 8 2018
a) f(5) = 2; f(1) = 0; f(0) không tồn tại; f(-1) không tồn tại.
b) Để hàm số được xác định thì \(x-1\ge0\Leftrightarrow x\ge1\)
c) Gọi x0 là số bất kì thỏa mãn \(x\ge1\). Khi đó ta có:
\(h\left(x_0\right)=f\left[\left(x_0+1\right)-1\right]-f\left(x_0-1\right)=\sqrt{x_0}-\sqrt{x_0-1}\)
\(h\left(x_0\right)\left[f\left(x_0+1\right)+f\left(x_0\right)\right]=\left(\sqrt{x_0}-\sqrt{x_0-1}\right)\left(\sqrt{x_0}+\sqrt{x_0-1}\right)=x_0-\left(x_0-1\right)=1>0\)
Vì \(\sqrt{x_0}+\sqrt{x_0-1}>0\Rightarrow h\left(x_0\right)>0\)
Vậy thì với các giá trị \(x\ge1\) thì hàm số đồng biến.
10 tháng 7 2023
a: f(x)=3x^2
a=3>0
=>Hàm số đồng biến khi x>0 và nghịch biến khi x<0
b: f(1)=f(-1)=3*1^2=3
f(2)=3*2^2=12
f(-4)=3*(-4)^2=48
c: f(x)=48
=>x^2=48/3=16
=>x=4 hoặc x=-4
d;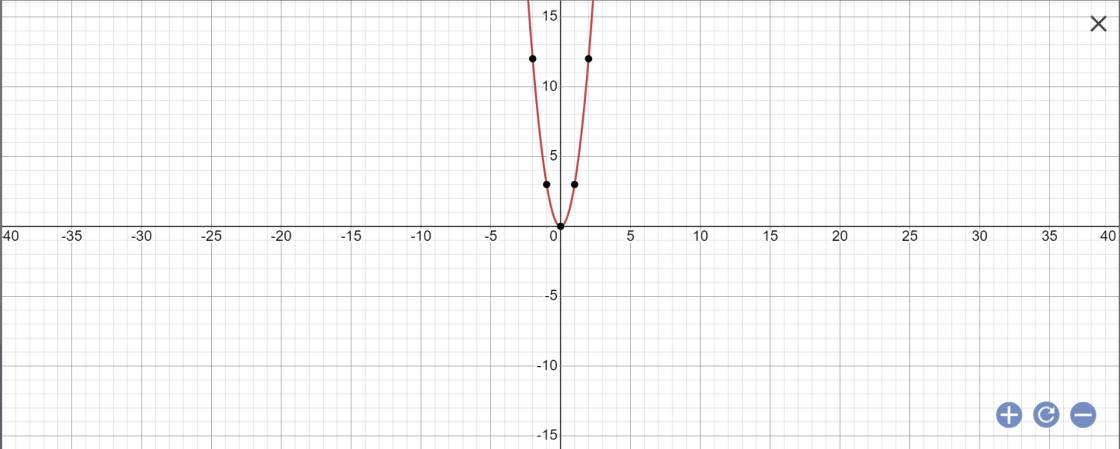 
C
0
15 tháng 11 2023
a: Thay x=1 và y=2 vào \(y=f\left(x\right)=ax^2\), ta được:
\(a\cdot1^2=2\)
=>a*1=2
=>a=2
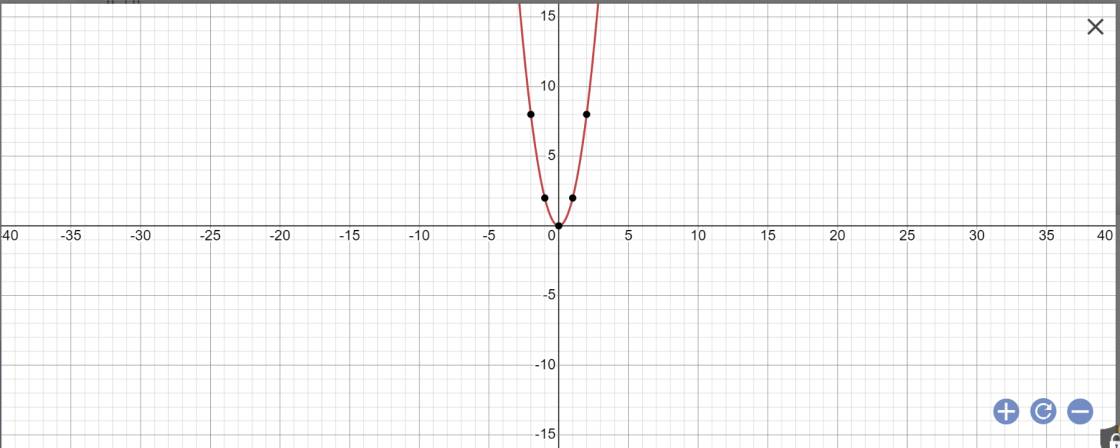
=>\(y=2x^2\)
b: bảng giá trị:
| x | -2 | -1 | 0 | 1 | 2 |
| \(y=2x^2\) | 8 | 2 | 0 | 2 | 8 |
Đồ thị:
1 tháng 2 2022
a: ĐKXĐ: (x+4)(x-1)<>0
hay \(x\notin\left\{-4;1\right\}\)
b: \(y-3=\dfrac{2x^2+6\sqrt{\left(x^2+1\right)\left(x-2\right)}+5-3x^2-9x+12}{x^2+3x-4}\)
\(=\dfrac{-x^2-9x+17+6\sqrt{\left(x^2+1\right)\left(x-2\right)}}{x^2+3x-4}< =0\)
=>y<=3
27 tháng 7 2017
Ta có \(f\left(x\right)+2f\left(\frac{1}{x}\right)=x\left(1\right)\)
Lại có \(f\left(\frac{1}{x}\right)+2f\left(x\right)=\frac{1}{x}\Rightarrow2f\left(\frac{1}{x}\right)+4f\left(x\right)=\frac{2}{x}\left(2\right)\)
Lấy (2)-(1) ta có \(2f\left(\frac{1}{x}\right)+4f\left(x\right)-2f\left(\frac{1}{x}\right)-f\left(x\right)=\frac{1}{x}-x\)
\(\Rightarrow3f\left(x\right)=\frac{2-x^2}{x}\Rightarrow f\left(x\right)=\frac{2-x^2}{3x}\)
Vậy \(f\left(x\right)=\frac{2-x^2}{3x}\)