Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
y = x + 1 - x 2 + 3 x x 2 + ( m + 1 ) x - m - 2 = ( x + 1 ) 2 - ( x 2 + 3 x ) ( x + 1 + x 2 + 3 x ) ( x - 1 ) ( x + m + 2 ) = - 1 ( x + 1 + x 2 + 3 x ) ( x + m + 2 )
+ Vì bậc tử số < bậc mẫu số nên luôn có một tiệm cận ngang y= 0
+ Vì phương trình x + 1 + x 2 + 3 x = 0 vô nghiệm nên chỉ có duy nhất một tiệm cận đứng nữa đó là đường thẳng x= -m-2.
Vậy với mọi x; đồ thị hàm số đã cho luôn có hai tiệm cận.
Chọn C.
\(\lim\limits_{x\rightarrow+\infty}\dfrac{2019x}{\sqrt{17x^2-1}-m\left|x\right|}=\lim\limits_{x\rightarrow+\infty}\dfrac{2019}{\sqrt{17-\dfrac{1}{x^2}}-m}=\dfrac{2019}{\sqrt{17}-m}\)
\(\lim\limits_{x\rightarrow-\infty}\dfrac{2019x}{\sqrt{17x^2-1}-m\left|x\right|}=\dfrac{2019}{m-\sqrt{17}}\)
Với \(m\ne\sqrt{17}\Rightarrow\) đồ thị hàm số luôn có 2 tiệm cận ngang
Với \(m=\sqrt{17}\) đồ thị hàm số ko có tiệm cận ngang
Xét phương trình: \(\sqrt{17x^2-1}=m\left|x\right|\)
- Với \(m< 0\Rightarrow\) pt vô nghiệm \(\Rightarrow\) ko có tiệm cận đứng \(\Rightarrow\) ĐTHS có tối đa 2 tiệm cận (ktm)
- Với \(m\ge0\)
\(\Leftrightarrow17x^2-1=m^2x^2\Leftrightarrow\left(17-m^2\right)x^2=1\)
+ Nếu \(\left[{}\begin{matrix}m\ge\sqrt{17}\\m\le-\sqrt{17}\end{matrix}\right.\) pt vô nghiệm \(\Rightarrow\) ĐTHS có tối đa 2 tiệm cận (ktm)
+ Nếu \(-\sqrt{17}< m< \sqrt{17}\) pt có 2 nghiệm \(\Rightarrow\) ĐTHS có 2 tiệm cận đứng
Vậy \(m=\left\{0;1;2;3;4\right\}\) có 5 phần tử
ĐKXĐ: \(0< x\le2\)
Miền xác định của hàm không chứa vô cùng nên hàm ko có tiệm cận ngang
\(\lim\limits_{x\rightarrow0^+}\frac{\sqrt{2-x}}{\left(x-1\right)\sqrt{x}}=-\infty\) nên \(x=0\) là tiệm cận đứng
\(\lim\limits_{x\rightarrow1}\frac{\sqrt{2-x}}{\left(x-1\right)\sqrt{x}}=\infty\) nên \(x=1\) là tiệm cận đứng
Hàm có 2 tiệm cận đứng khi và chỉ khi phương trình: \(x^2+2\left(m-1\right)x+m^2-2=0\) có 2 nghiệm phân biệt khác 1
\(\Leftrightarrow\left\{{}\begin{matrix}1+2\left(m-1\right)+m^2-2\ne0\\\Delta'=\left(m-1\right)^2-\left(m^2-2\right)>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m^2+2m-3\ne0\\-2m+3>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< \dfrac{3}{2}\\m\ne\left\{1;-3\right\}\end{matrix}\right.\)
1.
Để ĐTHS có 2 tiệm cận thì \(m\ne-3\)
Khi đó:
\(\lim\limits_{x\rightarrow\infty}\frac{mx-3}{x+1}=m\Rightarrow y=m\) là tiệm cận ngang
\(\lim\limits_{x\rightarrow-1}\frac{mx-3}{x+1}=\infty\Rightarrow x=-1\) là tiệm cận đứng
Giao điểm 2 tiệm cận có tọa độ \(A\left(-1;m\right)\)
Để A thuộc \(y=x+3\Leftrightarrow m=-1+3\Rightarrow m=2\)
2.
\(\lim\limits_{x\rightarrow+\infty}\frac{\sqrt{x-2}}{x^2-4}=0\Rightarrow y=0\) là 1 TCN
\(\lim\limits_{x\rightarrow2}\frac{\sqrt{x-2}}{x^2-4}=\infty\Rightarrow x=2\) là 1 TCĐ
\(x=-2\) ko thuộc TXĐ nên ko phải là tiệm cận
Vậy ĐTHS có 2 tiệm cận
3.
Để ĐTHS có đúng 2 TCĐ \(\Leftrightarrow x^2-mx+5=0\) có 2 nghiệm pb khác 1
\(\Leftrightarrow\left\{{}\begin{matrix}6-m\ne0\\\Delta=m^2-20>0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m\ne6\\\left[{}\begin{matrix}m\ge2\sqrt{5}\\m\le-2\sqrt{5}\end{matrix}\right.\end{matrix}\right.\)
\(\Rightarrow m=\left\{5;-5\right\}\)
Đề bài sai hoặc đáp án sai
ĐKXĐ: \(\left[{}\begin{matrix}x\ge2\\x\le-2\end{matrix}\right.\)
\(\lim\limits_{x\rightarrow-5}f\left(x\right)=\infty\) nên \(x=-5\) là 1 tiệm cận đứng
\(\lim\limits_{x\rightarrow+\infty}\frac{x\sqrt{x^2-4}}{\left(x-1\right)\left(x+5\right)}=\frac{\sqrt{1-\frac{4}{x^2}}}{\left(1-\frac{1}{x}\right)\left(1+\frac{5}{x}\right)}=1\)
\(\Rightarrow y=1\) là 1 TCN
\(\lim\limits_{x\rightarrow-\infty}\frac{x\sqrt{x^2-4}}{\left(x-1\right)\left(x+5\right)}=\frac{-\sqrt{1-\frac{4}{x^2}}}{\left(1-\frac{1}{x}\right)\left(1+\frac{5}{x}\right)}=-1\)
\(\Rightarrow y=-1\) là 1 TCN
Vậy ĐTHS đã cho có 3 đường tiệm cận (\(x=1\) ko thuộc TXĐ nên ko phải là TCĐ đâu)
2.
\(-x^3+3x^2=k\)
\(y=-x^3+3x^2\)
\(y'=-3x^2+6x\)
\(y'=0\Leftrightarrow x=0,x=2\)
Kẻ bảng biến thiên.
Đường thẳng y = k cắt đồ thị hàm số \(\Leftrightarrow0< k< 2\)
1.
ĐKXĐ: \(\left\{{}\begin{matrix}0\le x\le1\\x\ge2\end{matrix}\right.\)
\(\lim\limits_{x\rightarrow1^-}\frac{2x+3\sqrt{x}+1}{\sqrt{x^2-3x+2}}=\infty\Rightarrow x=1\) là TCĐ
\(\lim\limits_{x\rightarrow2^+}\frac{2x+3\sqrt{x}+1}{\sqrt{x^2-3x+2}}=\infty\Rightarrow x=2\) là TCĐ
\(\lim\limits_{x\rightarrow+\infty}\frac{2x+3\sqrt{x}+1}{\sqrt{x^2-3x+2}}=2\Rightarrow y=2\) là TCN
Vậy ĐTHS có 3 tiệm cận
3.
\(\lim\limits_{x\rightarrow0}y=\infty\Rightarrow x=0\) là TCĐ
\(\lim\limits_{x\rightarrow-\infty}\frac{\sqrt{x^2+2x+9}+\sqrt{1-x}}{x}=-1\Rightarrow y=-1\) là TCN
ĐTHS có 2 tiệm cận
4.
\(\lim\limits_{x\rightarrow-2^+}y=\infty\Rightarrow x=-2\) là TCĐ
ĐTHS có 1 TCĐ (\(x=-3\) ko thuộc TXĐ của hàm số nên đó ko phải là TCĐ)
.
.
Chọn D
Đồ thị hàm số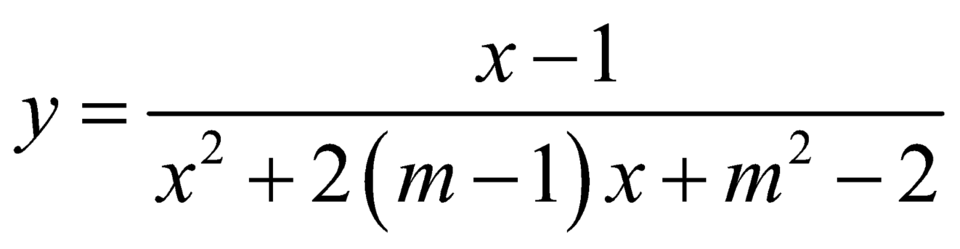 
có đúng hai tiệm cận đứng
có 2 nghiệm phân biệt khác 1.
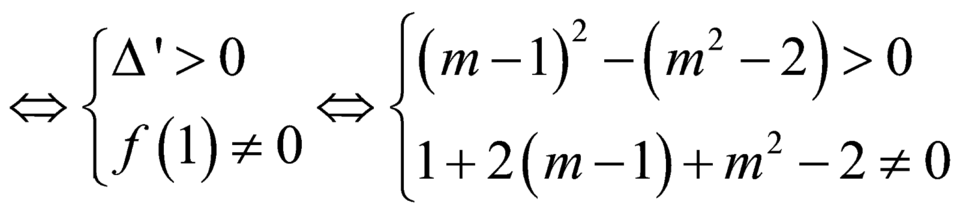
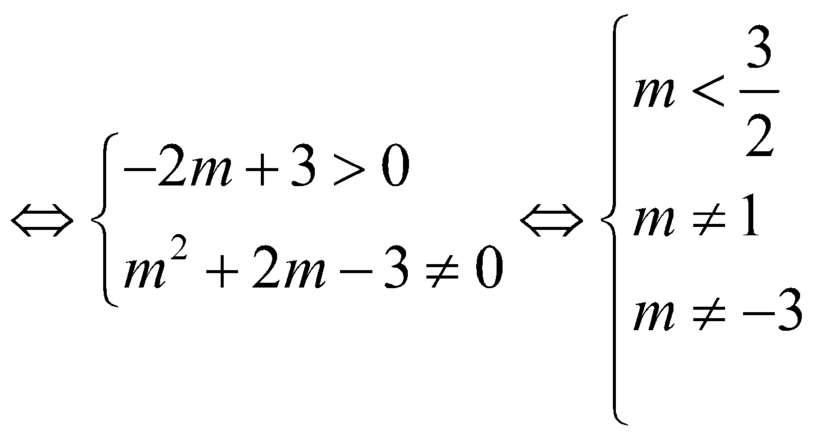
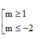
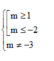
Do \(\lim\limits_{x\rightarrow\infty}\frac{x+1-\sqrt{x^2+3x}}{x^2+\left(m+1\right)x-m-2}=0\) với mọi m nên hàm số luôn có 1 tiệm cận ngang \(y=0\)
Để hàm số có đúng 2 tiệm cận thì nó có thêm đúng 1 tiệm cận đứng
Xét 2 hàm số:
\(\left\{{}\begin{matrix}g\left(x\right)=x+1-\sqrt{x^2+3x}\\f\left(x\right)=x^2+\left(m+1\right)x-m-2=\left(x-1\right)\left(x+m+2\right)\end{matrix}\right.\)
Do \(f\left(x\right)\) và \(g\left(x\right)\) có 1 nghiệm chung \(x=1\) nên bài toán thỏa mãn khi:
TH1: \(m+2=-1\Rightarrow m=-3\)
TH2: \(\left\{{}\begin{matrix}m\ne-3\\\left[{}\begin{matrix}-m-2\ge0\\-m-2\le-3\end{matrix}\right.\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m\ne-3\\\left[{}\begin{matrix}m\le-2\\m\ge1\end{matrix}\right.\end{matrix}\right.\)
Vậy \(\left[{}\begin{matrix}m\ge1\\m\le-2\end{matrix}\right.\)